Research Article - Der Pharma Chemica ( 2018) Volume 10, Issue 12
Synthesis and Equilibrium Investigation of the Interaction of Model Antitumour Palladium(Ii)Complex with Biorelevant Ligands
Haneen H AL-Gedany1*, Azza A Shoukry and Saedah R Al Mhayawi12Department of Chemistry, Faculty of Science, Cairo University, 12613 Giza, Egypt
Haneen H AL-Gedany, Department of Chemistry, Faculty of Science for Girls, 50918, Jeddah-21533, Kingdom of Saudi Arabia, Email: webmaster@kau.edu.sa
Abstract
For the purpose of finding additional metal based anticancer medications with lower toxicity and higher affectivity, Pd(byp)Cl2 complex, where byp is 2,2-bipyridine, was characterized and synthesized. The formed stable and Stoichiometric constants between different bimolecular targets (ligands) that have diverse functional groups and accessible in vivo such as, amino acids, amides, DNA unit constituents and [Pd(byp)(H2O)2]2+ were examined at constant ionic strength of 0.1 mol.dm-3 and at 25ºC. The diverse classes' concentrations were evaluated utilizing distribution diagrams. Moreover, the [Pd(byp)(H2O)2]2+ complexes with different chosen ligands were formed and characterized.
Keywords
2, 2´-bipyridine, Palladium(II), Biorelevant ligands, Stability constant.
Introduction
Metal based anticancer chemotherapy began at a clinical level in the late of 1970's with the utilization of cis-platin [1]. Although, cis-Platin is still in utilized today as carboplatin or iproplatin, which are portrayed by lower poisonous and higher affectivity against ovarian carcinomas, bladder tumors, head cancer etc. [2]; its clinical usage was restricted by unwanted side effects such as neurotoxicity, nephrotoxicity, ototoxicity, myelosuppression,vomiting and nausea that limit the dose that will be taken by patients [3].
Due to the noticed similarity of the coordination chemistry between Pd(II) and Pt(II) complexes and for the purpose of avoiding the toxicity of Pt(II) complexes, a group of labile Pd(II) have evidenced its usefulness as models of the reactions for the similar Pt(II) complexes.
Also, it was previously investigated that the combining of antitumor DNA binding agents with planar aromatic N-containing ligands including pyridine and its compounds would bring about promising results that observed to be valuable for improvement of new medications and DNA foot printing agents [4-6].
In view of the above realities and as a continuance of the researchers' past work on the binding interaction of DNA with metal complexes [7-9] and on the equilibrium of complex formation reactions of various biorelevant ligands with palladium(II) complexes [10,11], in this research the [Pd(byp)Cl2] will be characterized, synthesized and converted into the relating diaqua complex that was previously described to be active under physiological conditions that are linked adequately to various bio relevant ligands [12].
Materials and Methods
Materials and reagents
The materials that were utilized in conducting this research are: PdCl2, 2, 2´-bipyridine (byp), amino acids (L-alanine, L-valine L-phenylalanine, L-serine, L- threonine, L-histamine, methionine glycine, glutathione for analysis reduced, L-tyrosine, L-histidine, L(+)-ornithine.HCl and L(-)-tryptophan), peptides (glycylglycine, glycinamide.HCl, L(+)-glutamine and L-asparagine), dibasic acids(1-dicarboxylic (CBDCA), cyclobutane1, succinic, oxalic and malonic acid) and DNA units (uredines, uracil, inosine-5'-monophosphate, thymidine, thymine, adenosine, guanosine, adenine, inosine and guanosine-5' monophosphate) (Figure 1), in which all of the above reagents' solutions were prepared in deionized water. Also, in order to avoid the formulation of chloride ligand in solutions, hydrochloric derivatives were transformed into nitrate through the addition of AgNO3 and removing of AgCl.
Synthesis of the Complexes
[Pd(byp)Cl2] was prepared by heating 200.0 mg of PdCl2 in 168.2 mg of KCl and 40 ml of H2O. The solution of [PdCl4]2- was cooled, filtered and 2, 2´-bipyridine (Figure 2) ligand was added to the stirred solution. The pH was adjusted to 2-3. The precipitate of [Pd(byp)Cl2] was formulated then filtered and washed for three times with distilled water, diethyl and ethanol.
By treating [Pd(byp)Cl2] with two equivalents of AgNO3, it was transformed into the diaqua complexes [13], then the white formed AgCl precipitate was filtered. Great attention was given to the synthesize process in order to guarantee its freedom from Ag+ ion and the completely convertion of the complexes into diaqua species.
Synthesis of ternary complexes
The synthesis of ternary complexes was conducted through the mixing of 333.5 mg of [Pd(byp)Cl2] with 337.5 mg of AgNO3 in 10 ml H2O, the mixture was stirred for 24 hours in dark. Then the formed filtrate from the filtering off the AgCl precipitate was added to the following solutions: (104.06 mg) for malonic acid, (144.1 mg) for H2CBDCA, (392.17 mg) for inosine-5'-monophosphate, (90.03 mg) for oxalic acid and (75.07 mg) for glycine. The pH value was adjusted to 4.0-5.0. The precipitated complexes were isolated by vacuum filtration washed 3 times with diethyl ether, ethanol and H2O. Elemental hydrogen, nitrogen and carbon analyses were performed with a Perkin- Elmer 240 elemental analyzer as presented in Tables 1 and 2.
| Complexes Empirical formula | M. Wt | color | Yield % | Elemental analysis, found (calcd.) % | ||
|---|---|---|---|---|---|---|
| C | H | N | ||||
| [Pd(byp)(oxaliate)].H2O PdC12H10O5N2 | 350.42 | Yellowish white | 78 | 39.08 (41.09) |
2.71 (2.28) |
7.6 (7.99) |
| [Pd(byp)(malonate)].2H2O PdC13H12O5N2 | 364.42 | Yellowish white | 88 | 40.79 (42.8) |
3.13 (2.74) |
7.32 (7.68) |
| [Pd(byp)(glycinate)].H2O PdC12H15O3N3 | 337.42 | yellow | 94 | 40.51 (42.67) |
4.22 (3.85) |
11.81 (12.44) |
| [Pd(byp)(CBDCA)].H2O PdC16H16O5N2 | 404.42 | Yellow | 90 | 45.66 (41.09) |
3.78 (3.46) |
6.62 (7.99) |
| [Pd(bpy)(inosine-5-monophosphate)].2H2O PdC20H23O10N6p | 607.42 | Yellowish white | 92 | 37.3 (39.51) |
3.57 (3.12) |
13.05 (13.82) |
Table 1: Micro analytical data of the prepared metal complexes
| Complexes Empirical formula | Assigned wavenumbers (cm−1) | ||||||
|---|---|---|---|---|---|---|---|
| νO-H | δNH2 | νC-H | νsym C=O |
νasym C=O |
νpd-N | νpd-O | |
| [Pd(byp)(oxalate)].H2O | 3437 | 1288 | 3074 | 1357 | 1697 | 574 | 435 |
| [Pd(byp)(malonate)].2H2O | 3394 | 1265 | 3039 | 1450 | 1631 | 578 | 420 |
| [Pd(byp)(CBDCA)].H2O | 3437 | 1261 | 3043 | 1454 | 1635 | 570 | 470 |
| [Pd(byp)(glycinate).H2O | 3402 | 1230 | 3082 | 1365 | 1666 | 586 | 405 |
| [Pd(byp)(inosine-5-monophosphate)].H2O | 3421 | 1226 | 3113 | - | - | 509 | - |
Table 2: IR Spectral Data of the metal complexes
Potentiometric procedure and measurements
Potentiometric titrations were performed with Hi 902 automatic titrator. The electrode and titroprocessor were adjusted with standard buffer solutions that were prepared in accordance with NBS specification [14].
The subsequent mixtures (A-D) were synthesized and titrated potentiometrically: A) 40 ml of aqueous solution containing 5 × 10-3 M ligand (peptides, aminoacids, dibasic acids or DNA constituents) in order to obtain their acid dissociation constants, B) 40 ml aqueous solution containing (5 × 10-3 M) [Pd(byp)(H2O)2]2+ in order to obtain the hydrolysis constants of [Pd(byp)(H2O)2]2+, C) 40 ml aqueous solution containing (5 × 10-3 M) [Pd(byp)(H2O)2]2+ and dibasic acids, peptides or amino acids in order to obtain the complexes' formation constant, and lastly D) 40 ml aqueous solution containing(5 × 10-3 M) [Pd(byp)(H2O)2]2+ and (1 × 10-2 M) DNA constituents for the purpose of obtaining their formation constants too.
However, guanosine-5'-monophosphate, inosine-5'-monophosphate, adenosine and Adenine were prepared in the protonated form by dissolving in the required amount of Nitric Acid. The readings of pH meter were changed into concentration of hydrogen ion by titrating a standard acid solution. The pH is plotted against p[H]. So, the relationship pH-p[H]=0.05 was observed and [OH-] value was calculated using a pKw value of 13.997 [13].
Data processing
The calculations were made through ca.100 data points for each titration utilizing least squares computer program MINIQUAD-75 [15]. Through the trying of several potential composition models, the stability and stoichiometries constants for the complexes were obtained. The selected model represents the best statistical fit one. It was tested by contrasting the simulated theoretical curve computed from the he formation constant of the corresponding complex and the acid dissociation constants of the ligand, and the experimental titration data as given in Table 3. The complexation equilibria were illustrated from the concentration distribution curves acquired with the program SPECIES and under the experimental condition utilized [16].
| System | p | q | ra | logba | pKca | Sb |
|---|---|---|---|---|---|---|
| Pd(byp)-OH | 1 | 0 | -1 | - 3.88 (0.03) | ||
| 1 | 0 | -2 | - 13.01 (0.06) | 3.10E-08 | ||
| 2 | 0 | -2 | -4.46 (0.02) | |||
| Glycine | 0 | 1 | 1 | 9.60 (0.01) | 9.6 | 1.60E-07 |
| 0 | 1 | 2 | 11.93 (0.02) | 2.33 | ||
| 1 | 1 | 0 | 10.01 (0.05) | 3.70E-07 | ||
| Valine | 0 | 1 | 1 | 9.58 (0.01) | 9.58 | |
| 0 | 1 | 2 | 11.71 (0.02) | 2.13 | ||
| 1 | 1 | 0 | 11.03 (0.09) | 1.30E-06 | ||
| Alanine | 0 | 1 | 1 | 9.69 (0.01) | 9.69 | 9.30E-08 |
| 0 | 1 | 2 | 11.89 (0.007) | 2.2 | ||
| 1 | 1 | 0 | 11.01 (0.07) | 8.10E-07 | ||
| Methionine | 0 | 1 | 1 | 9.12 (0.02) | 9.12 | |
| 0 | 1 | 2 | 11.39 (0.03) | 2.27 | ||
| 1 | 1 | 0 | 12.30 (0.06) | 8.90E-07 | ||
| Phenylalanine | 0 | 1 | 1 | 9.12 (0.01) | 9.12 | 2.00E-08 |
| 0 | 1 | 2 | 11.01 (0.03) | 1.89 | ||
| 1 | 1 | 0 | 11.79 (0.02) | 7.70E-08 | ||
| Serine | 0 | 1 | 1 | 9.14 (0.01) | 9.14 | |
| 0 | 1 | 2 | 11.40 (0.02) | 2.26 | ||
| 1 | 1 | 0 | 9.13 (0.05) | |||
| 1 | 1 | -1 | 1.71 (0.07) | 7.42 | 9.30E-08 | |
| Tryptophan | 0 | 1 | 1 | 9.52 (0.01) | 9.52 | 3.20E-08 |
| 1 | 1 | 0 | 12.50 (0.06) | 2.37E-07 | ||
| 1.00E-08 | ||||||
| Ornithine | 0 | 1 | 1 | 10.58 (0.00) | 10.58 | 1.60E-07 |
| 0 | 1 | 2 | 19.44 (0.01) | 8.86 | ||
| 0 | 1 | 3 | 21.39 (0.02) | 1.95 | ||
| 1 | 1 | 0 | 12.67 (0.08) | 9.70E-07 | ||
| 1 | 1 | 1 | 20.79 (0.04) | 8.12 | ||
| Tyrosine | 0 | 1 | 1 | 10.18 (0.002) | 10.18 | 1.10E-08 |
| 0 | 1 | 2 | 19.42 (0.003) | 9.24 | 8.20E-07 | |
| 0 | 1 | 3 | 22.28 (0.02) | 2.86 | ||
| 1 | 1 | 0 | 16.43 (0.13) | |||
| 1 | 1 | -1 | 7.81 (0.11) | 8.62 | 1.00E-07 | |
| Histidine | 0 | 1 | 1 | 9.53 (0.01) | 9.53 | 1.80E-07 |
| 0 | 1 | 2 | 15.81 (0.02) | 6.28 | 1.50E-07 | |
| 1 | 1 | 0 | 14.80 (0.07) | |||
| Histamine | 0 | 1 | 1 | 9.59 (0.01) | 9.59 | 2.90E-08 |
| 0 | 1 | 2 | 15.65 (0.02) | 6.06 | ||
| 1 | 1 | 0 | 13.00 (0.11) | 5.00E-07 | ||
| Threonine | 0 | 1 | 1 | 9.06 (0.01) | 9.06 | 7.90E-08 |
| 0 | 1 | 2 | 11.03 (0.02) | 1.97 | ||
| 1 | 1 | 0 | 9.45 (0.08) | 1.10E-06 | ||
| 1 | 1 | -1 | 0.84 (0.04) | 8.61 | ||
| Glutathione | 0 | 1 | 1 | 9.63 (0.01) | 9.63 | 2.90E-08 |
| 0 | 1 | 2 | 18.33 (0.01) | 8.7 | ||
| 0 | 1 | 3 | 21.84 (0.01) | 3.51 | ||
| 1 | 1 | 0 | 15.88 (0.12) | 2.50E-07 |
al, p, q and r are the stoichiometric coefficients corresponding to PdII, byp, other ligand and H+ respectively; bStandard deviation are given in parentheses; cSum of square of residuals
Table 3: Formation constants for complexes of [Pd(byp)(H2O)2]2+ with amino acids at 25ºC and 0.1 M ionic strength
Effect of solvent
The initial phase in calculations was to change over the pH-meter readings (B) recorded in dioxane– water into hydrogen particle fixation [H+]. This can be accomplished by utilizing the broadly utilized Van Uitert and Hass equation shown below:
-log10[H+] = B + log10 UH (1)
Four different mixtures were prepared and titrated potentiometrically. The four mixtures had a volume of 40 ml in dioxane-water solutions of different compositions (0.05, 0.1, 0.15 and 0.2 mol.dm-3) and 0.1 M ionic strength (adjusted with NaNO3). A standard 0.05 M NaOH solution was used as the titrant. The pH meter readings were converted to hydrogen ion concentration by titrating a standard HNO3 solution (0.01 M), the ionic strength of which was adjusted to 0.1 M with NaNO3, with standard NaOH (0.05 M) at 25°C.
Effect of chloride
The proton association constants of the CBDCA ligand, the hydrolysis constants of [Pd(byp)(H2O)2]2+ and the formation constants of Pd(byp)-CBDCA at different ionic strength were determined potentiometrically by titrating the 5 mixtures that are made from 40 ml of solution containing 5 × 10-3 mol.dm-3 [Pd(byp)(H2O)2]2+, 3.30 × 10-3 mol.dm-3 CBDCA, at different ionic strengths starting from 0.05 mol.dm-3 NaCl (2 ml × 5.0 mol.dm-3 NaNo3), through 0.1 mol.dm-3 NaCl (4 ml × 5.0 mol.dm-3 NaNo3), 0.15 mol.dm-3 NaCl (6 ml × 5.0 mol.dm 3 NaNo3), 0.20 mol.dm-3 NaCl (8 ml × 5.0 mol.dm-3 NaNo3) and ending with 0.25 mol.dm-3 NaCl (10 ml × 5.0 mol.dm-3 NaNO3).
Effect of temperatures
The formation constants of Pd(byp)-CBDCA at different temperatures were determined using potentiometric data obtained from the mixture of 40 ml of solution containing 5 × 10-3 mol.dm-3 [Pd(byp)(H2O)2]2+, 3.30 × 10-3 mol.dm-3 CBDCA of constant ionic strength 0.05 mol.dm-3 dioxane (5 ml × 5.0 mol.dm-3 NaNo-3).
Results and Discussions
Acid-base equilibria of [Pd(byp)(H2O)2]2+ complex
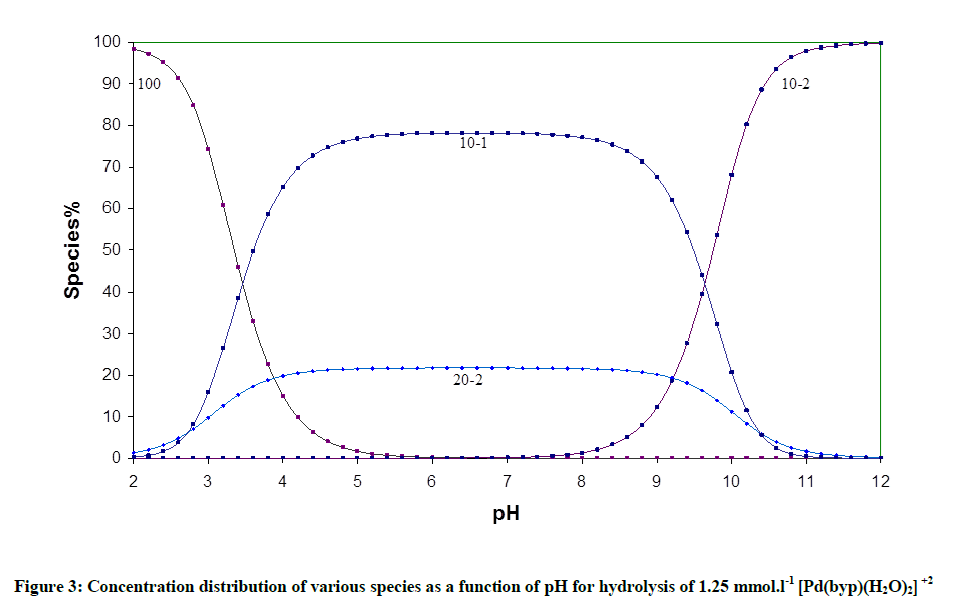
The acid- base chemistry of [Pd(byp)(H2O)2]2+ was described by fitting data Figure 3 to various acid-base models. The best-fit model was obtained to be stable with three species: 10-1, 10-2 and 20-2. The 10-1 and 10-2 species are because of the elimination of protonation of the two coordinated water molecules shown in equations (2) and (3). The third species, 20-2, is the dimeric species of di-μ-hydoxy complex (10-1) combined with [Pd(byp)(H2O)2]2+ species (100) as in equation (4).
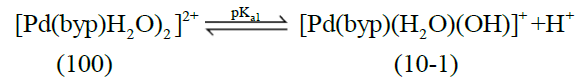 (2)
(2)
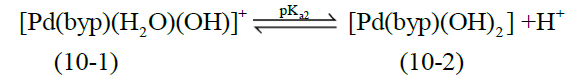 (3)
(3)
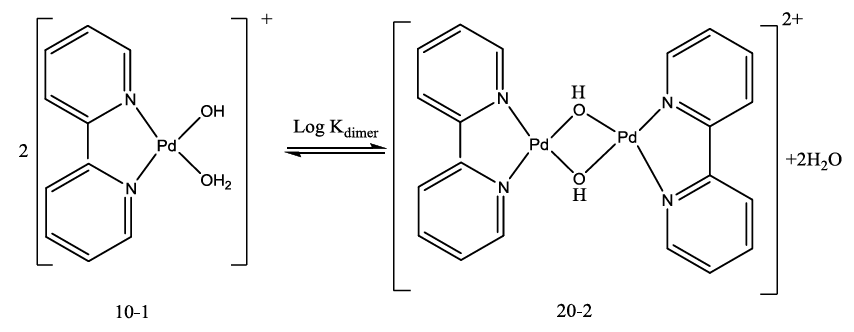 (4)
(4)
The concentration distribution diagram for [Pd(byp)(H2O)2]2+ and its hydrolyzed species are shown in Figure 3. The [10-1 species] increase as long as pH is increasing until it reaches maximum concentration of 78.18% at pH 6.4. An additional increment in pH is followed by an increment in the dihydroxo species (10-2), which is the main species above pH ~ 8.40.
Complex formation equilibria involving amino acids
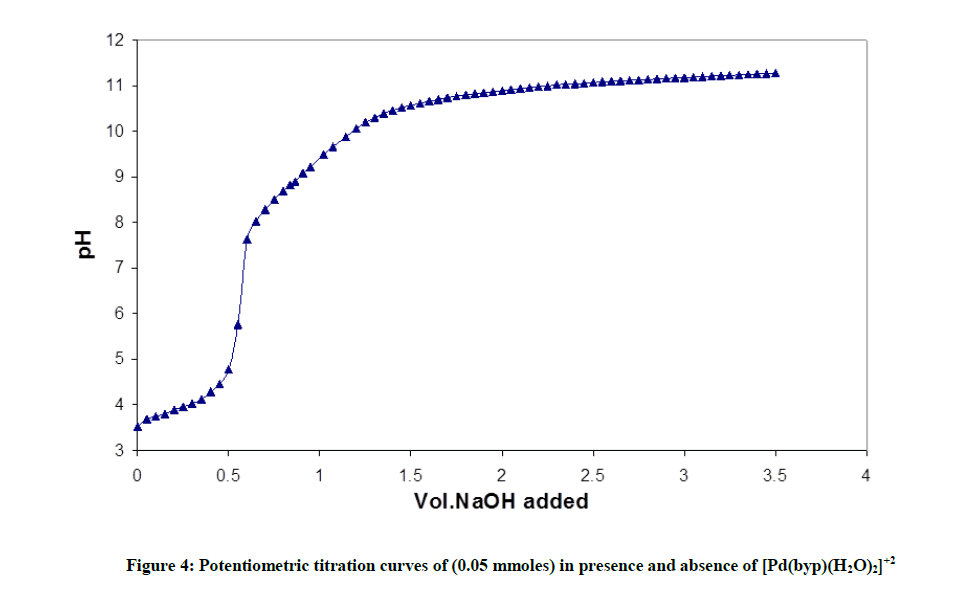
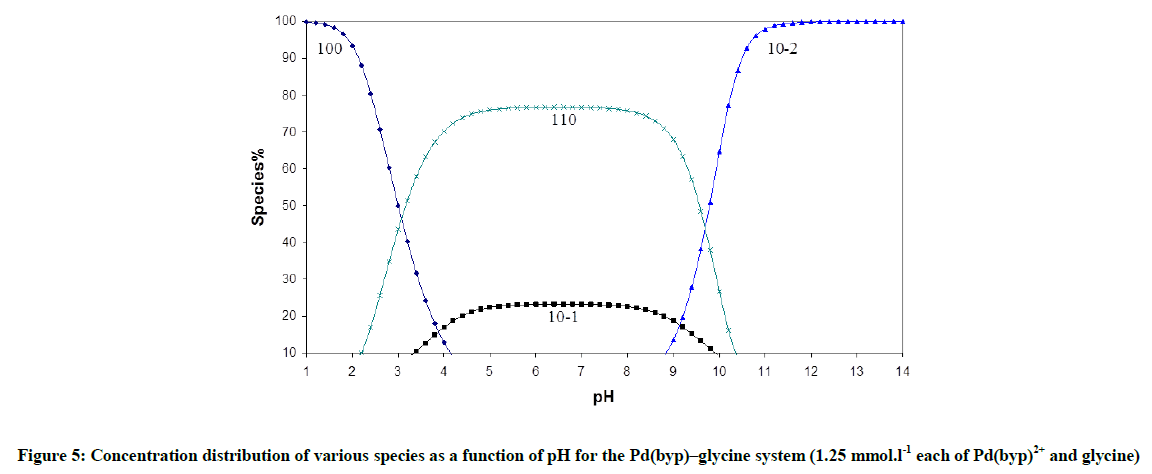
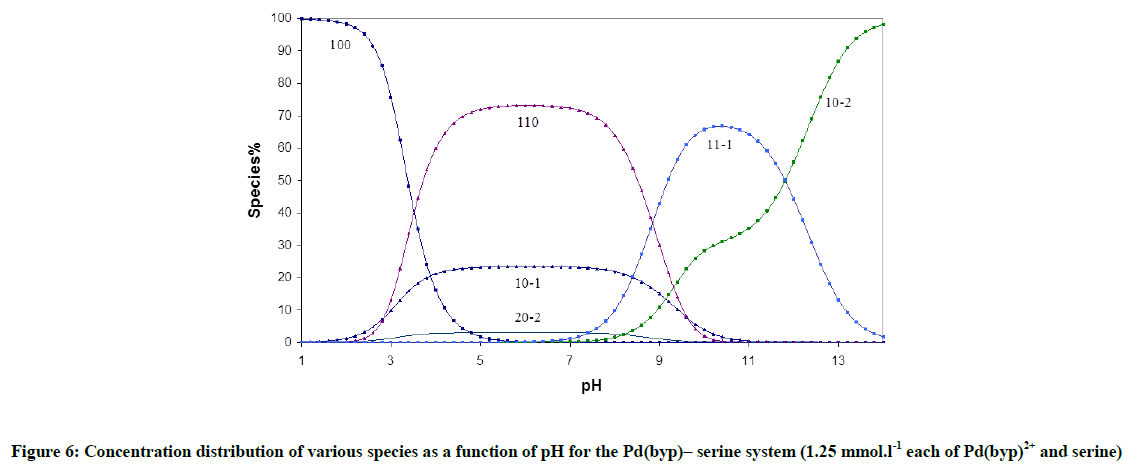
Fitting of the potentiometric data (Figure 4) for [Pd(byp)]–amino acid equilibria indicates formation of 1: 1 complexes. It was found that [Pd(byp)(H2O)2]2+ encourages the ionization of the alcohol group of glycine and serine (Figures 5 and 6) in the presence of the species 11-1 indicates the ionization of the OH side-chain. The pKa of the ionization is calculated from the following equation: pKa=log β110 - log β11-1 (5), in which pKa values of threonine and serine, obtained with Pd(byp) are 7.71 and 7.24 respectively, see in Table 3. This value is lower than that of the Pd(N,N´ dimethylethylenediamine)-serine complex (8.43) [17-19]. This may be due the π-acceptor property of the pyridine ring, which increases the electrophilicity of the Pd(II) ion and consequently decreases the pKa value of the coordinated alcoholate group.
The formation constant value of the (110) species is in fair agreement with that of histamine complex, but higher than those of α-amino acids. This indicates that histidine interacts with [Pd(byp)(H2O)2]2+ in the same way as histamine does i.e. through the amino and imidazole. The stability constant of the Pd(byp)-ornithine complex (logβ110=12.67) is higher than those of α- amino acids. This may indicate that ornithine most likely chelates by the two amino groups at higher pH, this is being supported by the great affinity of palladium to nitrogen donor centres. However, the stability constant of the (110) complex (log β=15.88) is higher than the ones of α-amino acids (log β[Pd(byp)(glycine)]=10.01). This indicates that glutathione interacts with Pd(II) ion by the deprotonated SH and amino groups and not by the carboxylate and amino group like simple α-amino acids. This is in good agreement with the fact that Pd(II) has a high affinity for S-donor ligands.
Complex Formation Equilibria Involving Amides
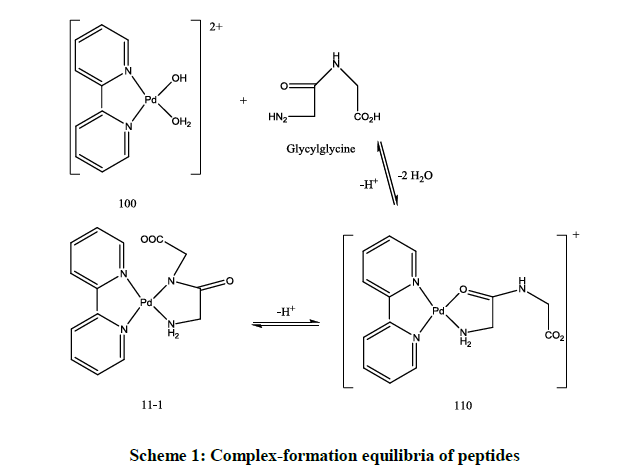
Peptides form complexes with stochiometric coefficients 110 and 11-1 as shown in the following Scheme 1.
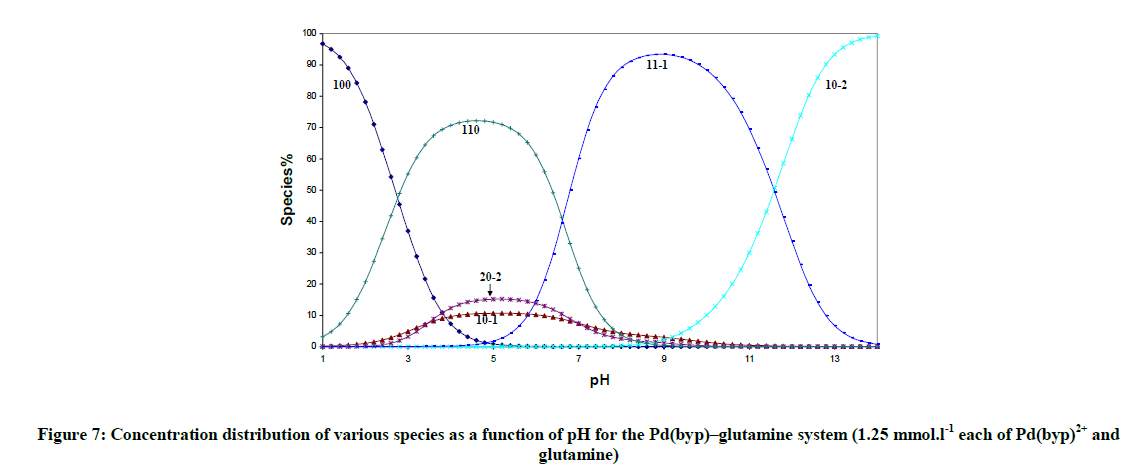
According to Table 4, the stability of the complex with glycylglycine (log β110) is generally higher than glycinamide. The electrostatic interaction between doubly positively charged palladium complex and the negatively charged glycylglycine would result in a lowering of free energy of formation. Glutamine and Aspargine complexes have the highest stability; this is may be because of the presence of α- NH2 that can coordinate first (glycine-like). Also, the stability of aspargine is higher and its pKa of the peptide NH is lower than that of glutamine due to larger chelate ring size in case of glutamine.
| System | p | q | ra | logba | pK ca | Sb |
|---|---|---|---|---|---|---|
| Glycinamide | 0 | 1 | 1 | 7.88 (0.00) | 7.88 | 4.60E-08 |
| 1 | 1 | 0 | 6.79 (0.44) | |||
| 1 | 1 | -1 | 2.64 (0.06) | 4.15 | 2.00E-06 | |
| Glycylglycine | 0 | 1 | 1 | 7.94 (0.01) | 7.94 | 2.50E-08 |
| 1 | 1 | 0 | 7.52 (0.66) | |||
| 1 | 1 | -1 | 2.94 (0.15) | 4.58 | 1.10E-06 | |
| Aspargine | 0 | 1 | 1 | 8.55 (0.01) | 8.55 | 5.90E-08 |
| 1 | 1 | 0 | 9.03 (0.53) | |||
| 1 | 1 | -1 | 3.86 (0.06) | 5.17 | 1.50E-07 | |
| Glutamine | 0 | 1 | 1 | 7.96 (0.01) | 7.96 | 1.10E-08 |
| 1 | 1 | 0 | 7.96 (0.14) | |||
| 1 | 1 | -1 | 1.34 (0.19) | 6.62 | 1.30E-06 |
al, p, q and r are the stoichiometric coefficients corresponding to PdII, byp, other ligand and H+ respectively; bStandard deviation are given in parentheses; cSum of square of residuals
Table 4: Formation constants for complexes of [Pd(byp)(H2O)2]2+ with peptides at 25ºC and 0.1 M ionic strength
The concentration distribution diagrams in Figure 7 indicate that all peptides form the complex species (110), at low pH and the hydrolysis of Pd (II) species is suppressed, i.e. the species (10-1) has a minor contribution. The species (11-1) is the main species at higher pH and it starts to form after pH is equal to 4.8, 4.8, 3.8, and 3.2 for aspargine, glutamine, glycylglycine and glycinamide respectively. This is the same order of decreasing stability of the complex with peptides.
Dicarboxylic Acid Complexes
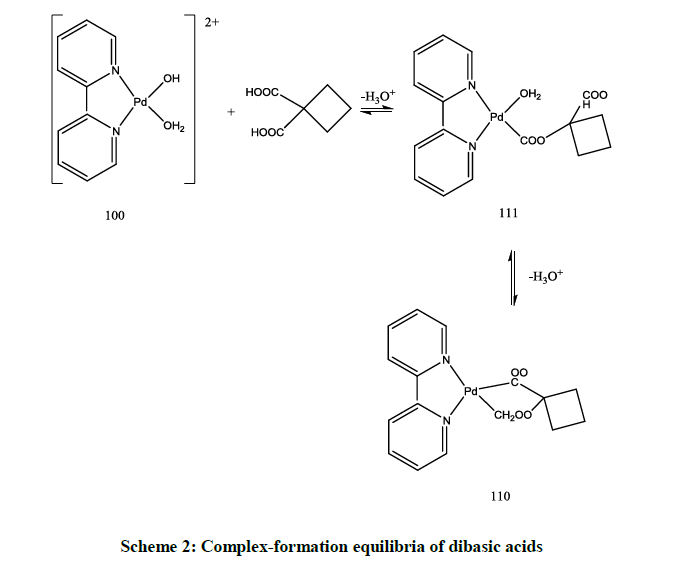
The dissociation constants of malonic, cyclobutane -1, 1- dicarboxylic, succinic and oxalic acids are shown in Table 5. The potentiometric data for a mixture solution of [Pd(byp)(H2O)2]2+ and dibasic acids, were fitted considering the formation of 110 and the monoprotonated complex species 111 according to Scheme 2.
| System | P | q | ra | logβb | pK ca | Sc |
|---|---|---|---|---|---|---|
| 1,1-CBDCA | 0 | 1 | 1 | 5.54 (0.01) | 5.54 | 0.000000087 |
| 0 | 1 | 2 | 8.77 (0.01) | 3.23 | 0.00000033 | |
| 1 | 1 | 0 | 8.15 (0.07) | |||
| 1 | 1 | 1 | 11.51 (0.13) | 3.36 | 0.00000055 | |
| Oxalic acid | 0 | 1 | 1 | 4.10 (0.01) | 4.1 | 1.3E-09 |
| 0 | 1 | 2 | 5.78 (0.06) | 1.68 | 0.00000037 | |
| 1 | 1 | 0 | 8.27 (0.04) | |||
| 1 | 1 | 1 | 11.67 (0.07) | 3.4 | 0.00000001 | |
| Malonic acid | 0 | 1 | 1 | 5.42 (0.01) | 5.42 | 0.000000028 |
| 0 | 1 | 2 | 8.19 (0.01) | 2.77 | ||
| 1 | 1 | 0 | 7.46 (0.06) | |||
| 1 | 1 | 1 | 10.70 (0.10) | 3.24 | 0.00000002 | |
| Succinic acid | 0 | 1 | 1 | 5.35 (0.00) | 5.35 | 0.000000018 |
| 0 | 1 | 2 | 9.41 (0.01) | 4.06 | 0.0000014 | |
| 1 | 1 | 0 | 5.40 (0.02) | |||
| 1 | 1 | 1 | 8.14 (0.02) | 2.74 | 0.00000002 |
p, q and ra are the stoichiometric coefficients corresponding to Pd(byp), dibasic acid and H+ respectively; bStandard deviation are given in parentheses; cSum of square of residuals. d, taken from ref. 101
Table 5: Formation constants for complexes of [Pd(byp)(H2O)2]2+ with Dibasic Acids at 25ºC and 0.1 M ionic strength
The results in Table 5 show that the stability constant of the 1: 1 complex having seven membered ring as in succinic acid is lower than five and six membered chelate rings as in cyclobutane dicarboxylic acid, malonic acid and oxalic acid complexes.
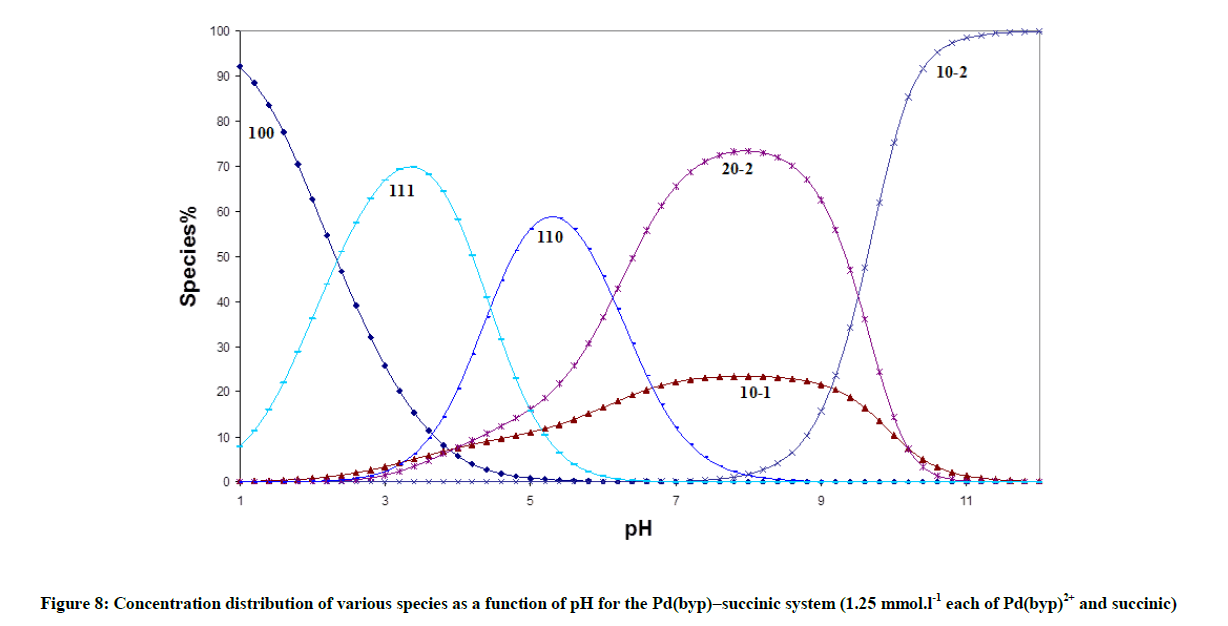
The concentration distribution diagrams in Figure 8 in appendix show that the species 111 is stable only at a low pH. The main species in the physiological pH range is the chelate structure, 110, species. The concentration of the monohydroxo, 10-1, is decreased and its maximum concentration is predominated at higher pH compared to [Pd(byp)(H2O)2]2+ (Figure 1). However, the dihydroxo species, 10-2, was not affected.
Complex Formation Equilibria Involving DNA Constituents
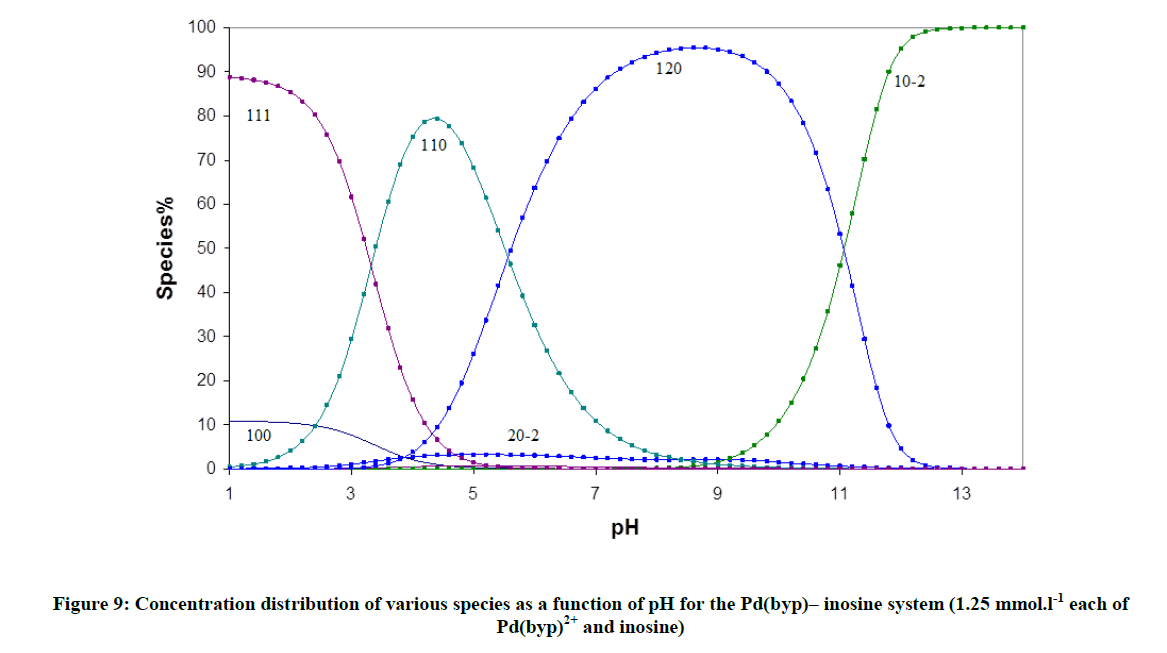
The accepted models for DNA complex formation with [Pd(byp)(H2O)2]2+ are consistent with the formation of 1: 2 and 1: 1 complexes (Tables 4 and 5). The pyrimidines, thymine and uracil have only basic nitrogen donor atoms (N3-C4O group). The protoated complexes are noticed at low pH for inosine and the whole monophosphate derivatives of DNA. Guanosine and Inosine can be protonated at N7 forming a (N1H-N7H) monocation. The pKa of N1H is 8.43 and 9.12 respectively for inosine (Figure 9), Table 6. The results showed that inosine and guanosine form the complexes 110, 111 and 120, while inosine-5'-monophosphate and guanosine-5'-monophosphate form 110, 111, 112 and 120, complexes. The pKa of the protonated form (logβ111- logβ110) amounts to 5.71 and 4.04. In case of IMP and GMP complexes, the protonated species formed correspond to N7 coordinated complex, where the N1 nitrogen and the phosphate group are protonated.
| System | P | q | ra | log bb | pK ca | Sc |
|---|---|---|---|---|---|---|
| Uracil | 0 | 1 | 1 | 9.28 (0.006) | 9.28 | 2.4E-08 |
| 1 | 1 | 0 | 8.39 (0.17) | 2.7E-07 | ||
| 1 | 2 | 0 | 14.05 (0.17) | |||
| Uridine | 0 | 1 | 1 | 9.01 (0.01) | 9.01 | 1.1E-07 |
| 1 | 1 | 0 | 8.26 (0.46) | 0.0000013 | ||
| 1 | 2 | 0 | 13.94 (0.46) | |||
| Thymine | 0 | 1 | 1 | 9.58 (0.00) | 9.58 | 8.7E-08 |
| 1 | 1 | 0 | 8.44 (0.32) | 6.3E-08 | ||
| 1 | 2 | 0 | 14.16 (0.13) | |||
| Thymidine | 0 | 1 | 1 | 9.50 (0.00) | 9.5 | 8.1E-08 |
| 1 | 1 | 0 | 8.30 (0.04) | 4.1E-08 | ||
| 1 | 2 | 0 | 14.09 (0.08) | |||
| Inosine | 0 | 1 | 1 | 8.43 (0.01) | 8.43 | 4.1E-08 |
| 1 | 1 | 0 | 8.76 (0.28) | 0.0000006 | ||
| 1 | 1 | 1 | 12.08 (0.28) | 3.32 | ||
| 1 | 2 | 0 | 14.66 (0.11) | |||
| Inosine 5'-monophosphate | 0 | 1 | 1 | 9.21 (0.01) | 9.21 | 4.3E-08 |
| 0 | 1 | 2 | 15.21 (0.01) | 6 | ||
| 1 | 1 | 0 | 10.01 (0.29) | 0.0000063 | ||
| 1 | 1 | 1 | 15.72 (2.46) | 5.71 | ||
| 1 | 1 | 2 | 20.29 (0.62) | 4.57 | ||
| 1 | 2 | 0 | 19.40 (2.46) | |||
| Guanosine | 0 | 1 | 1 | 9.12 (0.01) | 9.12 | 6.7E-08 |
| 1 | 1 | 0 | 9.30 (0.08) | 2.1E-07 | ||
| 1 | 1 | 1 | 13.40 (0.03) | 4.1 | ||
| 1 | 2 | 0 | 14.00 (0.01) | |||
| 1 | 2 | 1 | 19.86 (0.04) | 5.86 | ||
| Guanosine 5'-monophosphate | 0 | 1 | 1 | 9.28 (0.01) | 9.28 | 6.6E-08 |
| 0 | 1 | 2 | 15.41 (0.01) | 6.13 | 9.7E-07 | |
| 1 | 1 | 0 | 11.55 (0.19) | |||
| 1 | 1 | 1 | 15.59 (0.74) | 4.04 | ||
| 1 | 1 | 2 | 19.02 (0.45) | 3.43 | ||
| 1 | 2 | 0 | 20.69 (0.64) | |||
| 1 | 2 | 1 | 26.61 (0.47 | 5.92 | ||
| Adenine | 0 | 1 | 1 | 9.29 (0.01) | 9.29 | 9.4E-08 |
| 0 | 1 | 2 | 13.32 (0.02) | 4.03 | ||
| 1 | 1 | 0 | 10.72 (0.40) | 4.7E-08 | ||
| 1 | 1 | 1 | 15.53 (0.31) | 4.81 | ||
| 1 | 2 | 0 | 15.36 (0.16) | |||
| 1 | 2 | 1 | 24.76 (0.20) | 9.4 | ||
| Adenosine | 0 | 1 | 1 | 3.60 (0.01) | 3.6 | |
| 1 | 1 | 0 | 6.99 (0.04) | 3.26E-08 | ||
| 1 | 1 | 1 | 10.22 (0.05) | 3.23 | ||
| 1 | 2 | 0 | 14.31 (0.03) | |||
| 1 | 2 | 1 | 17.78 (0.07) | 3.47 |
p, q and ra are the stoichiometric coefficients corresponding to Pd(byp), DNA and H+ respectively; bStandard deviation are given in parentheses; cSum of square of residuals. d, taken from ref.101
Table 6: Formation constants for complexes of [Pd(byp)(H2O)2]2+ with DNA-Unit consttents at 25 °C and 0.1 M ionic strength
The IMP and GMP complexes are more stable than those of the pyrimidines. This is due to the basis of different columbic forces operating between the ions resulting from the negatively charged phosphate group. Another contribution that makes the nucleotides to be more stability than the nucleosides is the hydrogen bonding between the phosphate and the exocyclic amine [20-23].
Effect of solvent on the stability constants
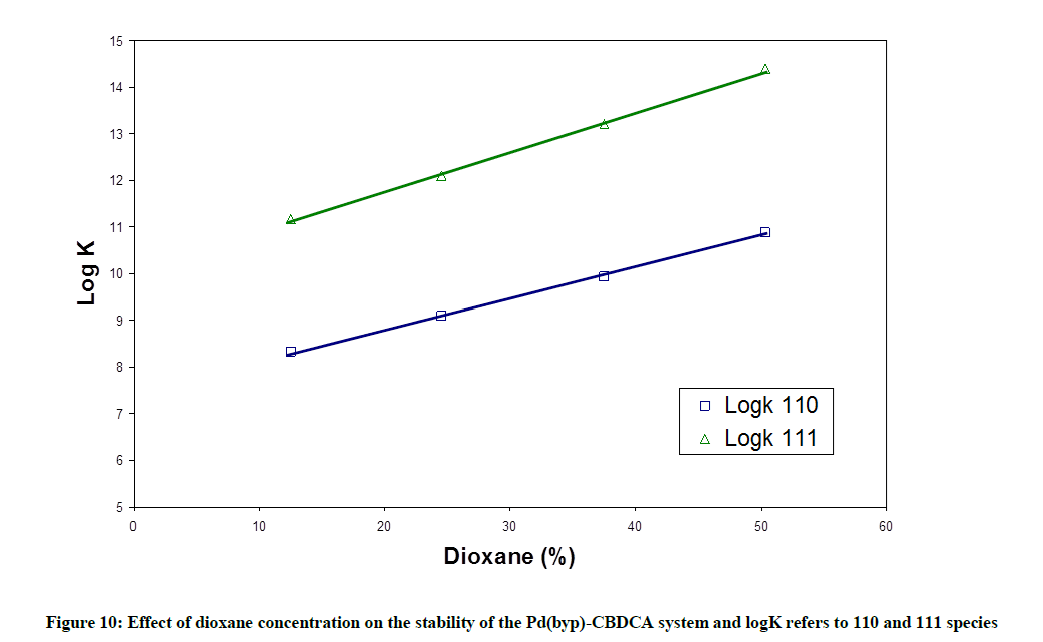
Although water has been considered as the solvent with best biological conditions, a lower polarity of it has been observed in some biochemical micro environment [24,25]. These properties relate nearly to those existed in dioxane/water mixtures. Accordingly, the study of the formation of Pd(byp)-CBDCA complex in water dioxane solution as a typical example could be biologically significant. To study this equilibra, all of the other equilibria involved, typically acid-base equilibria of [Pd(byp)(H2O)2]2+and CBDCA, must be investigated in similar solvent. The equilibrium constants are listed in Table 7. The hydrolysis of Pd(byp)2+ complex provides mono- and dihydroxy species. The increment in the concentration of dioxane will lead to an increment in pKa values of [Pd(byp)(H2O)2]2+ and CBDCA. This is due to the capability of solvent to increase the electrostatic attraction between the proton and hydrolyzed of Pd(II) species and between proton and ligand anion in case of CBDCA. The variation in stability constant of the CBDCA with [Pd(byp)(H2O)2]2+ complex is represented in appendices, in which it displays that an increment in dioxane (Figure 10) concentration increases stability constant of Pd(byp)-CBDCA complex due to the preference of complex formation in low dielectric constant that is represented by the increment of dioxane concentration.
| Dioxane (%) | M | L | Ha | Logβb Pd(byp) |
|---|---|---|---|---|
| 0% | 1 | 0 | -1 | -3.88(0.03) |
| 1 | 0 | -2 | -13.01 (0.06) | |
| 2 | 0 | -2 | -4.46 (0.02) | |
| 0 | 1 | 1 | 5.57(0.01) | |
| 0 | 1 | 2 | 8.57(0.02) | |
| 1 | 1 | 0 | 8.11(0.07) | |
| 1 | 1 | 1 | 11.46(0.13) | |
| 12.50% | 1 | 0 | -1 | -4.11(0.03) |
| 1 | 0 | -2 | -13.09 (0.08) | |
| 2 | 0 | -2 | -5.04 (0.02) | |
| 0 | 1 | 1 | 5.73(0.01) | |
| 0 | 1 | 2 | 8.75(0.01) | |
| 1 | 1 | 0 | 8.33(0.15) | |
| 1 | 1 | 1 | 11.19(0.19 | |
| 25% | 1 | 0 | -1 | -4.18(0.03 |
| 1 | 0 | -2 | -13.10 (0.07 | |
| 2 | 0 | -2 | -5.13 (0.02 | |
| 0 | 1 | 1 | 6.18(0.01 | |
| 0 | 1 | 2 | 9.71(0.01 | |
| 1 | 1 | 0 | 9.00(0.03 | |
| 1 | 1 | 1 | 12.02(0.06 | |
| 37.50% | 1 | 0 | -1 | -4.24(0.03 |
| 1 | 0 | -2 | -13.19 (0.09 | |
| 2 | 0 | -2 | -5.27 (0.02 | |
| 0 | 1 | 1 | 6.85(0.01 | |
| 0 | 1 | 2 | 10.51(0.02 | |
| 1 | 1 | 0 | 9.86(0.05 | |
| 1 | 1 | 1 | 13.03(0.07 | |
| 50 | 1 | 0 | -1 | -4.28(0.08 |
| 1 | 0 | -2 | -13.29 (0.10 | |
| 2 | 0 | -2 | -5.37 (0.02 | |
| 0 | 1 | 1 | 6.99(0.01 | |
| 0 | 1 | 2 | 11.30(0.01 | |
| 1 | 1 | 0 | 10.93(0.06 | |
| 1 | 1 | 1 | 14.60(0.09 |
aM, L and H are the stoichiometric coefficients corresponding to Pd(byp), CBDCA, and H+ respectively; bStandard deviations are given in parentheses; sum of square of residuals are less than 5 × 10-7
Table 7: Formation constants for the complex of [Pd(byp)(H2O)2]2+ with CBDCA at different concentrations of solvent (dioxane) and at 25ºC and 0.1 M ionic strength
Effect of chloride on the stability constants
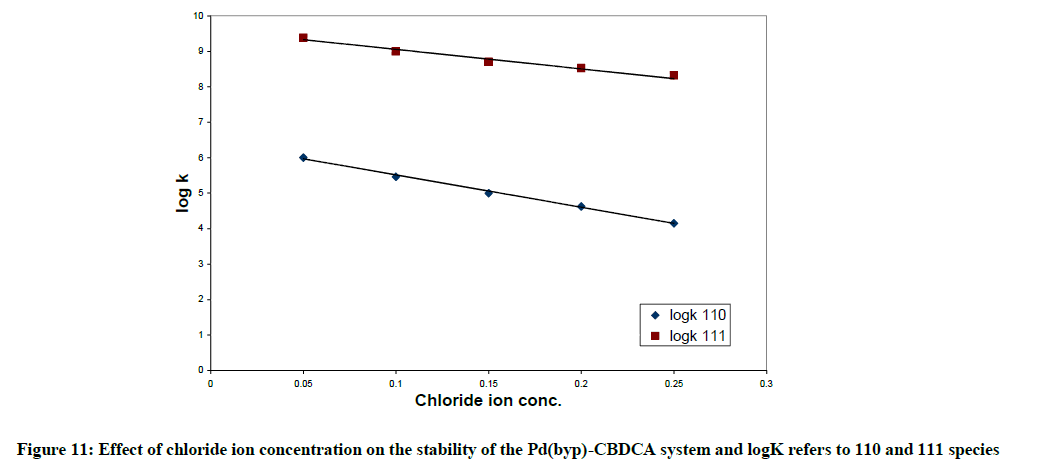
As the chloride ion concentration increases, the pKa values for the first and second coordinated water molecules of [Pd(byp)(H2O)2]2+ increase as represented in Table 6. This is due to the competition amongst OH- ion and chloride ion for reaction with [Pd(byp)(H2O)2]2+. The Pd(byp)-CBDCA complex 's equilibrium constants determined for various concentration of chloride ion concentrations with constant ionic strength are listed in Table 8. Those stability constants decrease with the increment of chloride ion concentration; this is explained on the premise that diaqua and mono- complexes decrease with increasing [Cl-] which affects stability of complexes. Also, Figures 11-14 represents the variation in stability constant of the Pd(byp)2+ complex with CBDCA as a function of Cl- ion concentration.
| [Cl-] mol L-1 | M | L | Ha | Logβb Pd(byp) | pK ca |
|---|---|---|---|---|---|
| 0 | 1 | 0 | -1 | -3.88(0.03) | 3.88 |
| 1 | 0 | -2 | -13.01 (0.06) | 9.13 | |
| 2 | 0 | -2 | -4.46 (0.02) | ||
| 1 | 1 | 0 | 8.11 (0.07) | ||
| 1 | 1 | 1 | 11.46 (0.13) | 3.35 | |
| 0.05 | 1 | 0 | -1 | -4.39 (0.16) | 4.39 |
| 1 | 0 | -2 | -13.55 (0.17) | 9.16 | |
| 2 | 0 | -2 | -4.99 (0.02) | ||
| 1 | 1 | 0 | 6.00 (0.26) | ||
| 1 | 1 | 1 | 9.38 (0.51) | 3.38 | |
| 0.1 | 1 | 0 | -1 | -4.57 (0.07) | 4.57 |
| 1 | 0 | -2 | -14.24 (0.08) | 9.67 | |
| 2 | 0 | -2 | -5.34 (0.02) | ||
| 1 | 1 | 0 | 5.46 (0.18) | ||
| 1 | 1 | 1 | 9.00 (0.16) | 3.54 | |
| 0.15 | 1 | 0 | -1 | -4.86 (0.02) | 4.86 |
| 1 | 0 | -2 | -14.58 (0.03) | 9.72 | |
| 2 | 0 | -2 | -5.56 (0.02) | ||
| 1 | 1 | 0 | 5.00 (0.24) | ||
| 1 | 1 | 1 | 8.70 (0.17) | 3.70 | |
| 0.2 | 1 | 0 | -1 | -5.33 (0.02) | 5.33 |
| 1 | 0 | -2 | -15.41 (0.03) | 10.08 | |
| 2 | 0 | -2 | -5.72 (0.02) | ||
| 1 | 1 | 0 | 4.62 (0.22) | ||
| 1 | 1 | 1 | 8.52 (0.16) | 3.90 | |
| 0.25 | 1 | 0 | -1 | -5.51 (0.08) | 5.51 |
| 1 | 0 | -2 | -15.73 (0.13) | 10.22 | |
| 2 | 0 | -2 | -5.98 (0.02) | ||
| 1 | 1 | 0 | 4.15 (0.19) | ||
| 1 | 1 | 1 | 8.32 (0.13) | 4.17 |
aM, L and H are the stoichiometric coefficients corresponding to to [Pd(byp)(H2O)2]2+, CBDCA, and H+ respectively; blogβ of to [Pd(byp)(H2O)2]1-CBDCA; Standard deviations are given in parentheses; sum of square of residuals are less than 6 × 10-8
Table 8: Formation constants for complexes of [Pd(byp)(H2O)2]2+ with CBDCA at different concentrations of chlorides at 25°C and 0.10 M ionic strength
Effect of temperature on the stability constants
The pKa values for byp at 35, 30, 25, 20 and 15ºC are listed in Table 9. The parameters ΔHo and ΔSo associated with the dissociation were calculated by van’t Hoff relation.
| Temp. (ºC) | M | L | Ha | Logβb Pd(byp) |
|---|---|---|---|---|
| 15 | 1 | 0 | -1 | -3.95(0.07) |
| 1 | 0 | -2 | -13.83 (0.13) | |
| 2 | 0 | -2 | -4.46 (0.02) | |
| 0 | 1 | 1 | 5.65 (0.01) | |
| 0 | 1 | 2 | 8.66 (0.01) | |
| 1 | 1 | 0 | 8.42 (0.06) | |
| 1 | 1 | 1 | 11.55 (0.07) | |
| 20 | 1 | 0 | -1 | -3.95 (0.07) |
| 1 | 0 | -2 | -13.38 (0.13) | |
| 2 | 0 | -2 | -4.46 (0.02) | |
| 0 | 1 | 1 | 5.65 (0.01) | |
| 0 | 1 | 2 | 8.66 (0.01) | |
| 1 | 1 | 0 | 8.42 (0.06) | |
| 1 | 1 | 1 | 11.55 (0.07) | |
| 25 | 1 | 0 | -1 | -3.91 (0.02) |
| 1 | 0 | -2 | -13.23 (0.06) | |
| 2 | 0 | -2 | -4.35 (0.02) | |
| 0 | 1 | 1 | 5.59 (0.01) | |
| 0 | 1 | 2 | 8.62 (0.01) | |
| 1 | 1 | 0 | 8.39 (0.07) | |
| 1 | 1 | 1 | 11. 34 (0.17) | |
| 30 | 1 | 0 | -1 | -3.83 (0.02) |
| 1 | 0 | -2 | -12.72 (0.04) | |
| 2 | 0 | -2 | -4.12 (0.02) | |
| 0 | 1 | 1 | 5.54 (0.01) | |
| 0 | 1 | 2 | 8.52 (0.01) | |
| 1 | 1 | 0 | 8.09 (0.02) | |
| 1 | 1 | 1 | 10.47 (0.03) | |
| 35 | 1 | 0 | -1 | -3.74 (0.02) |
| 1 | 0 | -2 | -12.69 (0.04) | |
| 2 | 0 | -2 | -4.00 (0.02) | |
| 0 | 1 | 1 | 5.50 (0.01) | |
| 0 | 1 | 2 | 8.48 (0.02) | |
| 1 | 1 | 0 | 7.91 (0.03) | |
| 1 | 1 | 1 | 10.24 (0.05) |
aM, L and H are the stoichiometric coefficients corresponding to [Pd(byp)(H2O)2]2+, CBDCA, and H+ respectively; blog β of [Pd(byp)(H2O)2]1-CBDCA. Standard deviations are given in parentheses; sum of square of residuals are less than 5 × 10-7
Table 9: Formation constants for complexes of [Pd(byp)(H2O)2]2+ with CBDCA at different temperatures and 0.10 M ionic strength
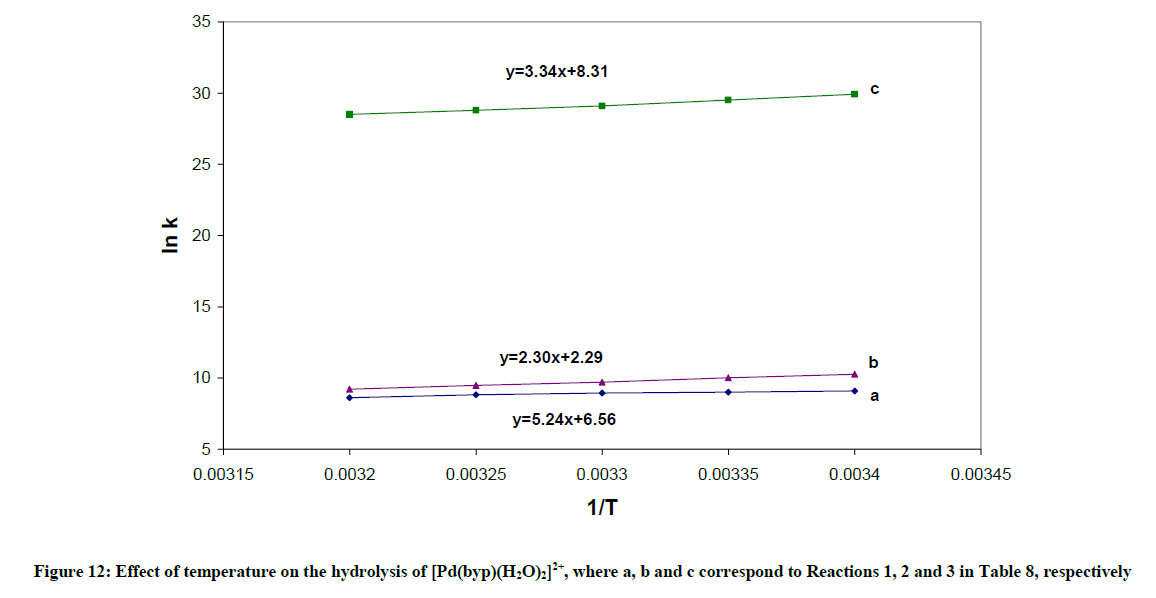
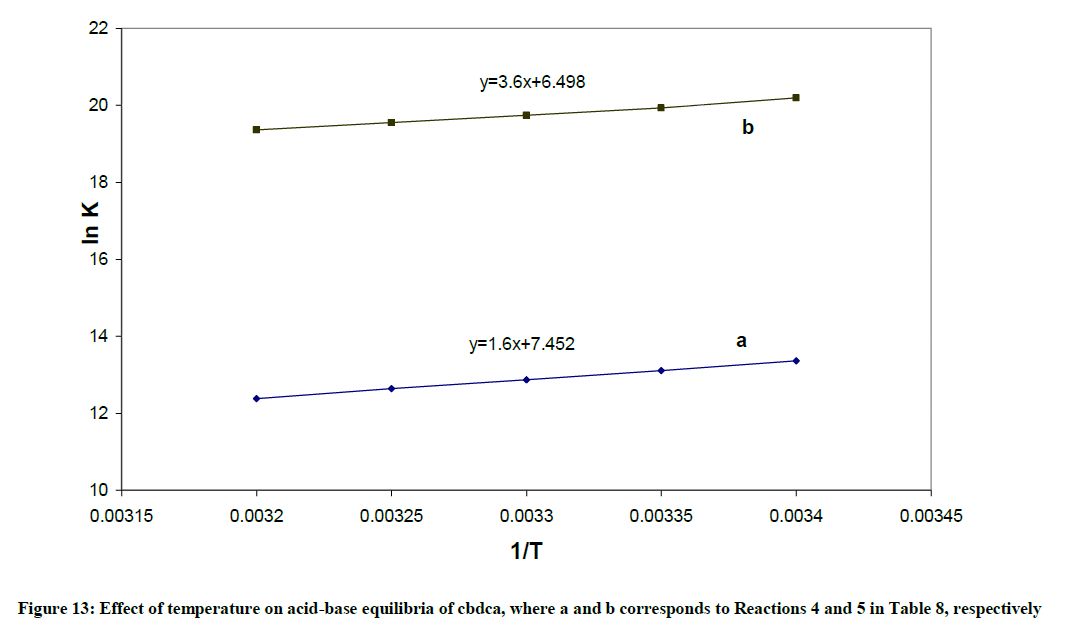
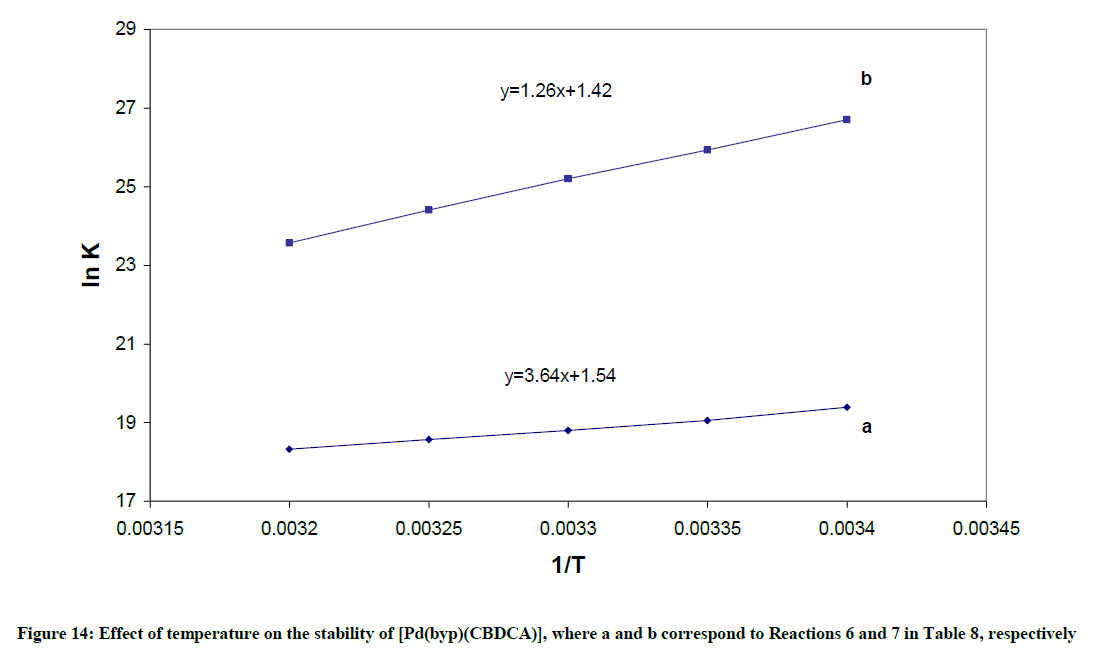
1) The formation constant for the [Pd(byp)(OH)]+, expressed as βOH, can be calculated from: log βOH=pKw + log β11-1. The hydrolysis reactions are complemented with endothermic liberation of water with an increment in entropy. The ΔHo values in Table 10 represent the net summation of the endothermic liberation of ordered water of hydration and the exothermic hydrolysis reaction. The hydrolysis reaction 1, which is an attraction between OH- and divalent cation, and reaction 2, which is attraction between OH- and monocation in Table 10 are exothermic reactions. Reaction 1 is more exothermic than reaction 2 and ΔSo value of Reaction 1 is higher than that of reaction 2.
| Equilibriumb | ΔH (kJ mol-1) | ΔS (kJ-1 mol-1) |
|---|---|---|
| Pd(byp)(H2O)22+ | ||
| 1) M(H2O)22++OH- M(H2O)(OH)+ + H2O | -43.56 (0.99) | 54.54 (0.98) |
2) M(H2O)(OH)+ + OH- 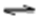 M(OH)2+ H2O M(OH)2+ H2O |
-19.12 (0.81) | 19.10 (0.83) |
3) 2M(H2O)(OH)+ 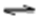 M2(OH)22+ +2H2O M2(OH)22+ +2H2O |
-27.77 (0.98) | 69.12 (0.99) |
| CBDCA | ||
4) L2- + H+ 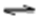 LH- LH- |
-13.30 (0.96 | 61.50 (0.96) |
5) LH- + H+ 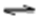 LH2 LH2 |
-5.48 (0.98) | 54.02 (0.98) |
6) M(H2O)22+ + L2- 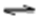 ML +2H2O ML +2H2O |
-30.26 (0.98) | 12.80(0.98) |
7) ML + H+ 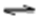 M(LH)+ M(LH)+ |
-10.47 (0.99) | 11.80 (0.99) |
aM denotes Pd(byp) and L denotes ligand; Standard deviations are given in parentheses; bStepwise formation constants
Table 10: Thermodynamic parameters for the equilibria of Pd(byp) complexes
2) The protonation reactions 4 and 5 of CBDCA in Table 10 are exothermic with negative ΔH values, since they are all neutralization reactions.
3) The complexation reaction 6 is exothermic with a negative ΔH value. This is because of the neutralization between the negative ligand and positive Pd(byp)2+ species.
Conclusion
In conclusion, we have prepared a new series of ligands based on the byp is 2,2-bipyridine, where byp is 2,2-bipyridine, Pd(byp)Cl2 complex was characterized and synthesized. The investigation describes the formation equilibria of [Pd(byp)(H2O)2]2+ with ligands of biological significance. The results show that amino acids form highly stable complexes, the formation constant value of the (110) species is in fair agreement with that of histamine complex, but higher than those of α-amino acids. This indicates that histidine interacts with [Pd(byp)(H2O)2]2+ in the same way as histamine does i.e. through the amino and imidazole. The stability constant of the Pd(byp)-ornithine complex (logβ110=12.67) is higher than those of α- amino acids. This may indicate that ornithine most likely chelates by the two amino groups at higher pH, this is being supported by the great affinity of palladium to nitrogen donor centers. However, the stability constant of the (110) complex (log β=15.88) is higher than the ones of α-amino acids (log β[Pd(byp)(glycine)]=10.01).
The present study shows clearly that the [Pd(byp)(H2O)2]2+complex can form strong bonds with peptides and promote facile deprotonation of the peptide. All peptides form the complex species (110), at low pH and the hydrolysis of Pd (II) species is suppressed, i.e. the species (10-1) has a minor contribution.
The species (11-1) is the main species at higher pH and it starts to form after pH is equal to 4.8, 4.8, 3.8, and 3.2 for aspargine, glutamine, glycylglycine and glycinamide respectively. This is the same order of decreasing stability of the complex with peptides.
Among the dicarboxylic acid ligands it may be concluded that, CBDCA forms the most stable complex, which is inconsistent with the fact that CBDCA complexes have the highest antittumor activity.
In addition, CBDCA forms the ring opened mono-protonated complex which may interact with DNA, i.e. the main target for antitumor. From a combination of stability constant data of such diaqua complexes with dicarboxylic acids, amino acids, peptides and DNA constituents, it will in principle be possible to calculate the equilibrium distribution of the metal species in biological fluids where all types of ligands are present simultaneously.
References
- B. Rosenberg, Cancer Chemother. Rep. Part 1, 1975, 59, 589.
- L. Pinto, S.J. Lippard, Biochim. Biophys. Acta., 1985, 780, 167.
- J.A. Hickman, K.J. Scanlon, T.R. Tritton, S. Shionoya, Y. Lu, Cancer Res., 1986, 46, 3445.
- B. Lippert, (Edi.) Cisplatin, Chemistry and Biochemistry of a Leading Anticancer Drug, John Wiley & Sons, New York, 1999.
- H.C. Harder, B. Rosenberg, Int. J. Cancer., 1970, 6, 207.
- A. Shoukry, K.M. Alahmary, Monthly Chemicals., 2013, 144(8), 1117-1127.
- A. Shoukry, J. Solution Chem., 2014, 43, 746-762.
- A. Shoukry, Indian Academy of Sciences., 2013, 125(3), 643-651.
- A. Shoukry, Int. J. Basic Appl. Sci., 2013, 38-46.
- D.S. Gill, in Platinum Coordination Compounds in Cancer Chemotherapy, proceedings of the fourth international symposium, Burlington, (Eds.) Hacker, Douple, and Krakoff, 1983, 267.
- A.A. Shoukry, M. Brindell, D. Piotrowska, G. Stochel, R. Eldik, J. Biol. Inorg. Chem., 2007, 12(6), 809.
- A. Paul, S. Bhattacharya, Curr. Sci., 2012, 102(2), 212 .
- P. Gans, A. Sabatini, A. Vacca, Inorg. Chim. Acta., 1976, 18, 237-239.
- G. Cohen, H. Eisenberg, Biopolymers., 8, 1969, 45.
- K.E. Erkkila, D.T. Odom, J.K. Barton, Chem. Rev., 1999, 99, 2777.
- D.S. Sigman, A. Mazumder, D.M. Perrin, Chem. Rev., 1993, 93, 2295.
- F. Zhang, Q. Liu, J. Coord. Chem., 1993, 28, 197.
- H. Siegel, Angew. Chem. Int. Edn., 1975, 14, 394,
- H. Siegel, S.S. Massoud, N.A. Corfu, J. Am. Chem. Soc., 1994, 116, 2958.
- M. Planiadavar, C. Natavajan, Aust. J. Chem., 1980, 33, 737.
- M.M. Shoukry, E.M. Khairy, A. Saeed, Transition Metal Chem., 1989, 13, 37).
- R.W. Hay, C.Y. Quan, Polyhedron., 1995, 14, 869.
- A.H. Chakraborty, M.R. Rahman, Transition Metal Chem., 1993, 18, 545.
- Sabatini, A. Vacca, P. Gans, Talanta., 1974, 21, 53.
- E. Bottari, A. Braibanti, E. Rizzarelli, S. Sammartano, C. Serverini, A. Vacca, D.R. Williams, Annali. Di. Chim., 1978, 68, 813 .