Research Article - Der Pharma Chemica ( 2018) Volume 10, Issue 9
New Theoretical Descriptor for Computational Study by Using Quantum Methods
Lakbaibi Z1, Jaafar A2*, Tabyaoui M1, Ben El Ayouchia H3, Byadi S4 and Boussaoud A2
1University of Mohammed V Faculty of Sciences, Department of Chemistry, Laboratory of Materials, Nanoparticles and Environment, BP 1014 Avenue Ibn Batouta Rabat, Morocco
2Laboratory of Process, Signals, Industrial Systems and Computer Science, Superior School of Technology, Cadi Ayyad University, Dar Si-Aïssa road, 46000, BP 89, Safi, Morocco
3Laboratory of Analytical and Molecular Chemistry, Polydisciplinary Faculty of Safi, Cadi Ayyad University, Safi, Morocco
4Faculty of Chemistry and Chemical Technology, University of Ljubljana, Slovenia
- *Corresponding Author:
- Jaafar A
Laboratory of Process, Signals
Industrial Systems and Computer Science
Superior School of Technology
Cadi Ayyad University
Dar Si-Aïssa road, 46000, BP 89, Safi, Morocco
Abstract
Several theoretical approachs could not define clearly the strong local attacks between the electrophilic and nucleophilic reagent when the local attack was predicted in the various methodologies, the various solvents and by the various substituents of reagents. For this, we have proposed a new descriptor, named ΔZ. Indeed, when ΔZ difference is very weaker, the local interaction is very strong and vice versa. This descriptor serves to select the best methodology, the best solvent or the possible geometries of reagents. This descriptor has been succefully evaluated.
Keywords
DFT, local interactions, ΔZ descriptor.
Introduction
Several theoretical approaches have been developed to predict or justify local responsiveness. Among others, the approach proposed by Domingo [1], stipulate that the most local interaction must be between the highest value nuleophilicity center Nk of nucleophilic reagent and the highest value electrophilicity center ωK of electrophilic reagent. Indeed, electron transfer has taken place from the most nucleophilic center of the nucleophilic specie to the most electrophilic center of the electrophilic specie. This approach has recently aroused the interest of researchers since it gives relevant results that justify various reactions in organic chemistry. However, in case of a local attack correctly justified under several solvents effects, or by different methodologies (calculation basis, solvation,…) and by different substituent of reagents, the Domingo theory does not give an indicator that allows showing the case where the local attack is more stronger. So, the aim of this study is to propose a descriptor will allow us to select the best solvent, best methodology and best substituent that correspond to the strong interaction.
Theoretical Background
From a theoretical study, the electrophilic and nucleophilic character of organic and inorganic species can be characterized by using the reactivity indices defined within the conceptual DFT framework [2-9]. For the non-radical species, global reactivity indices such as chemical potentials (μ), chemical hardness (η) and global electrophilicity (ω); where μ=(εHOMO+εLUMO)/2, η=εLUMO−εHOMO and ω=μ2/2η have been calculated. Then, the global nucleophilicity N is expressed as N=εHOMO (nucleophile) − εHOMO (TCE); it is referred to tetracyanoethylene (TCE) because it presents the lowest HOMO energy for a large molecular series.
For the radical species, chemical potential μ°, chemical hardness η°, global electrophilicity ω° are calculated by the following formulas:
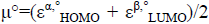 ,
, 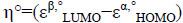 and
and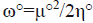 , where εα,° HOMO is the energy of one electron in α spin state of the frontier molecular orbital HOMO and εβ,° LUMO is the energy of one electron in β spin state of the frontier molecular orbital LUMO. On the other hand, the global nucleophilicity N° of the radical species is given as:
, where εα,° HOMO is the energy of one electron in α spin state of the frontier molecular orbital HOMO and εβ,° LUMO is the energy of one electron in β spin state of the frontier molecular orbital LUMO. On the other hand, the global nucleophilicity N° of the radical species is given as: 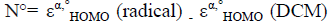 , where DCM is dicyanomethyl radical ((•CH(CN)2) is applied as a reference radical because it leads to positively scale of global nucleophilicity of radicals.
, where DCM is dicyanomethyl radical ((•CH(CN)2) is applied as a reference radical because it leads to positively scale of global nucleophilicity of radicals.
Power electroaccepting, ω+ (k), and power electrodonating, N- (k), for atom k of reagent are respectively estimated by the local electrophilic, P+K, and nucleophilic P-K ,Parr functions which are obtained from the analysis of the Mulliken atomic spin density (ASD) at the radical anion and at the radical cation by adding and removing an electron to the studied reagent, respectively. Note that 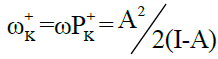 and
and 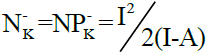 where A is the ability of an atom k to accept an electron density and I is the ability of an atom k to transfer its supplementary electron density to another electrophilic partner.
where A is the ability of an atom k to accept an electron density and I is the ability of an atom k to transfer its supplementary electron density to another electrophilic partner.
The quantum study is performed by the Gaussian 09 program package [10], and displayed with Gauss View [11].
Results and Discussion
According to an advanced bibliography, we can say that the local electrophilicity ω(k) is the affinity atoms to acquire an electron density. On the other hand, the local nucléophilicity N (k) is the power atoms to remove the supplementary electron density.
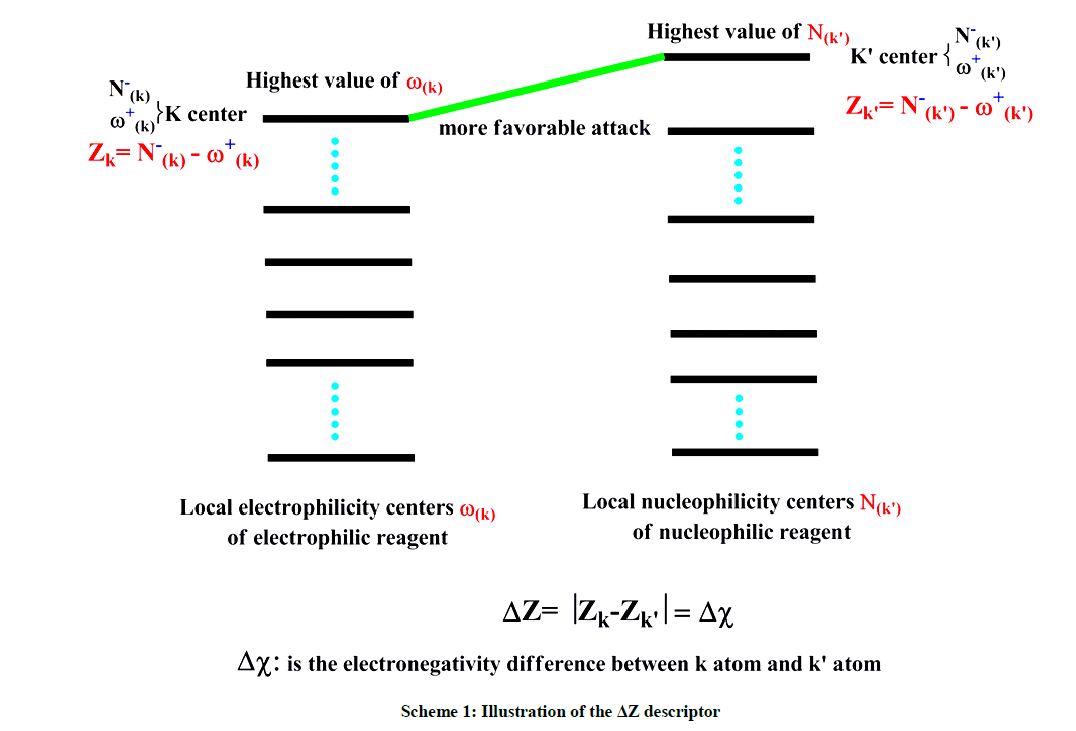
Therefore, for two reagents, the local attack is between the center has a highest electron affinity for the electrophilic reagent and the center has a highest electron density for a nucleophilic reagent. For a given local attack could be justified by several solvents, by changing the substituent of reagents and also by means computational methodologies; a reason that prompted us to propose a new descriptor, noted ΔZ. For a more favorable attack, noted k-k’, we have given the ΔZ descriptor by the following expression (Eq. 1):
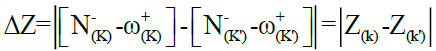 Eq. (1)
Eq. (1)
Where,
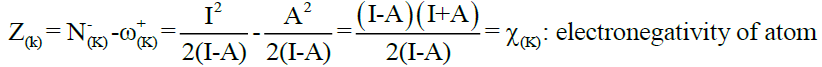 Eq. (2)
Eq. (2)
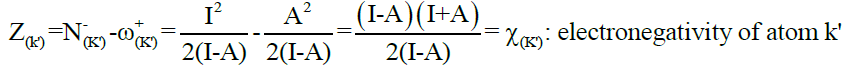 Eq. (2)
Eq. (2)
It is well noted that the concept of electronegativity has been exploited by numerous studies in order to investigate the nature of the bond formed between two atoms when two chemical species enter into reaction [12]. In the light of these discussions, we can evaluate the local interaction nature (strong or weak) by following the reasoning related to the concept of the electronegativity difference, i.e. ΔZ. Indeed, when the ΔZ difference is very weaker than the local interaction is very strong and vice versa. ΔZ descriptor is illustrated in Scheme 1. Consequently, this descriptor serves to select the best methodology, the best solvent or the possible geometries of reagents.
This descriptor has been successfully evaluated for some molecules that their formation due to different interactions already approved in literature, be it strong (for example F-F), moderate (for example H-F) or marginal (for example Li-F). Table 1 shows ΔZ values for an example of a non-polar covalent bond, polar covalent bond and ionic bond.
| Compound | Difluorine | Hydrogen fluoride | Lithium fluoride |
|---|---|---|---|
| F2 | HF | LiF | |
| Bond type | Non-polar covalent | Polar covalent | Ionic (non-covalent) |
| Z(k) (eV) | -8.51 | -8.51 | -8.51 |
| Z(k’) (eV) | -8.51 | -0. 454 | 3.138 |
| ∆Z (eV) | 0 | 8.056 | 11.648 |
Table 1: ΔZ values for an example of a non-polar covalent bond, polar covalent bond and ionic bond
According to the literature [12], the non-polar covalent bonds are stronger than the polar covalent and the ionic bonds is weaker than the covalent bonds. This is in good agreement with ΔZ values (Table 1).
Conclusion
The investigations could be deduced by the new descriptor ΔZ for a given local attack between two reactive sites are as follows:
• Know the best solvents that justify the local reactivity.
• Focus on methodologies that can be favorably adopted for the local responsiveness study.
• Choose the most suitable substituent associated to the reagents.
References
- L.R. Domingo, J.A. Saez, Org. Biomol. Chem., 2009, 7, 3576-3583.
- P. Geerlings, F.De Proft, W. Langenaeker, Chem. Rev., 2003, 103, 1793.
- L.R. Domingo, M. Rios-Gutérrez, P. Pérez, Molecules., 2016, 21, 748.
- R.G. Parr, L.V. Szentpaly, S. Liu, J. Am. Chem. Soc., 1999, 121, 1922.
- L.R. Domingo, E. Chamorro, P. Pérez, J. Org. Chem., 2008, 73, 4615.
- L.R. Domingo, P. Pérez, Org. Biomol. Chem., 2011, 9, 7168.
- W. Kohn, L.J. Sham, Phys. Rev., 1965, 140, 1133.
- W.Yang, W.J. Mortier, J. Am. Chem. Soc., 1986, 108, 5708.
- L.R. Domingo, P. Pérez, J.A. Saéz, RSC Adv., 2013, 3, 1486.
- M.J. Frisch, Gaussian 09, Gaussian Inc, Wallingford CT, 2009.
- R. Dennington, T. Keith, J. Millam, GaussView, Version 5, Semichem Inc., Shawnee Mission, KS.
- L. Pauling, The Nature of the Chemical Bond, 2nd (Edn.), Cornell University Press, Ithaca, 1940.