Research Article - Der Pharma Chemica ( 2024) Volume 16, Issue 6
Investigating the Validity of the New Equation of State for Predicting Pressure-Induced Changes in Halides at High Compression
Abhay P. Srivastava* and Brijesh K. PandeyAbhay P. Srivastava, Department of Physics and Material Science, MMM University of Technology, Gorakhpur (UP), India, Email: bkppms@mmmut.ac.in
Received: 15-Nov-2024, Manuscript No. DPC-24-152538; Editor assigned: 20-Nov-2024, Pre QC No. DPC-24-152538 (PQ); Reviewed: 04-Dec-2024, QC No. DPC-24-152538; Revised: 05-Dec-2024, Manuscript No. DPC-24-152538 (R); Published: 31-Dec-2024, DOI: 10.4172/0975-413X.16.6.531-534
Abstract
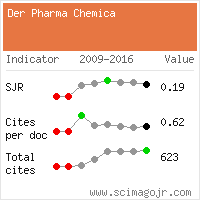
The Srivastava-Pandey Equation of State (EOS) represents a significant advancement in condensed matter physics, particularly in its application to semiconductors. This equation incorporates the theory of lattice potential and the concept of volume dependence of the short-range force constant. This equation contains a third-order approximation of the lattice potential, representing a notable advancement. A comprehensive comparative analysis was conducted, comparing the Srivastava-Pandey equation of state with previously derived equations of state. The results indicated that both the Vinet equation of state and the Srivastava-Pandey equation of state were consistent with experimental data for halides under high compression, demonstrating the robustness of the research. In contrast, the Murnaghan equation of state, Born-Mie equation of state, Holzapfel equation of state and Birch-Murnaghan equation of state exhibited less accuracy in calculating pressure at high compression. It was observed that the Vinet equation of state did not consistently match experimental findings for specific halides such as NaBr and NaI. Conversely, the Srivastava-Pandey EOS consistently produced results that matched the experimental data for all halide samples, highlighting its reliability and accuracy. This establishes a solid foundation for further research and applications, providing the scientific community with the latest advancements in the field.
Keywords
Equation of State (EOS); Srivastava-Pandey EOS; Vinet EOS; Murnaghan EOS; Holzapfel EOS; Born-Mie EOS;
Birch-Murnaghan EOS; Halides
Introduction
Studying ionic and mixed crystals under non-ambient conditions is a crucial aspect of materials science. These crystals, with their unique properties such as high melting points, electrical conductivity and optical properties, provide insightful information about their behavior in varied environments. This uniqueness makes them scientifically and technologically significant and researchers have devoted considerable attention to understanding their behavior under different conditions [1-7]. Our research has resulted in the development of a New Equation of State (NEOS) for halides, representing a substantial contribution to this field. Understanding materials' compression behavior is paramount for their diverse applications. The Equation of State (EOS) is crucial in comprehending this behavior. Several potentials and equations of state have been developed to estimate the compression behavior of solids and their thermoelastic properties. These properties hold immense significance in condensed matter physics, geophysics and ceramic sciences and our research aims to contribute to this understanding [8-10].
Materials and Methods
The EOS formulations are predicated on three thermodynamic parameters: Pressure (P), Volume (V) and Temperature (T). In our research, we have assessed the effectiveness of different equations of state, including Vinet EOS, Murnaghan EOS, Holzapfel EOS, Born-Mie EOS, Birch-Murnaghan EOS and a newly developed isothermal equation of state (NEOS), in calculating the pressure at different compressions. Our research seeks to provide a comprehensive understanding of the compression behavior of materials in varied conditions. We envision that our findings will significantly contribute to developing more accurate equations of state and potentials for predicting the behavior of materials under non-ambient conditions. This potential for further research and applications should inspire and motivate the scientific community for future work.
Results and Discussion
Srivastava and Pandey developed a new equation of state by utilizing the concept of the third-order approximation of lattice potential energy. In this study, calculations were extended to high compression values to validate the equation of state.
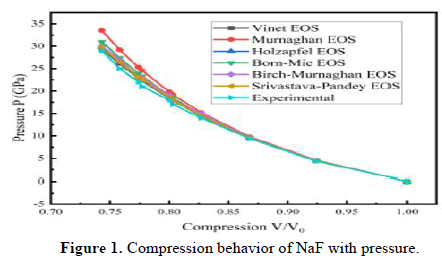
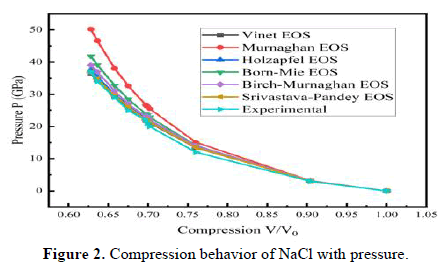
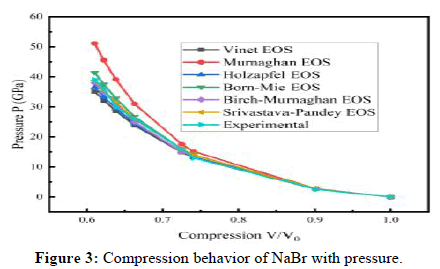
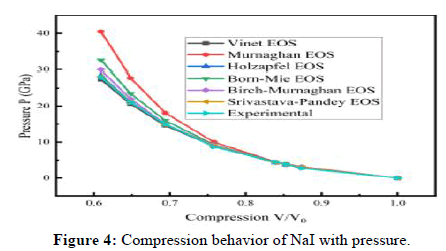
To evaluate how halides, behave under compression and verify the accuracy of specific equations, NaF, NaCl, NaBr and NaI samples were utilized, as experimental data for these samples were readily available. The input values required to calculate the compression behavior of the various halide samples are the isothermal bulk modulus at zero pressure (B0) and its pressure derivatives (B'). These values can be conveniently found in Table 1.
| Solids | B0 (GPa) | B'0 |
|---|---|---|
| NaF | 46.5 | 5.28 |
| NaCl | 24 | 5.39 |
| NaBr | 19.9 | 5.49 |
| NaI | 15.1 | 5.59 |
Table 1: Values of input data B0 (GPa), B0' (GPa) all at P=0.
The results obtained using different equations of state (EOS) for the selected halide samples can be found in Table 2. The pressure variations at various compression levels for the samples (NaF, NaCl, NaBr and NaI) are illustrated in Figures 1-4, including a comparison with experimental data. A comparative analysis of the various equations of state (EOS) shows that the Vinet EOS and Srivastava-Pandey EOS produce pressure values that are closer to the experimental results than the Murnaghan EOS, Holzapfel EOS, Born-Mie EOS and Birch-Murnaghan EOS. The analysis also shows that the Vinet EOS is suitable for some samples, while the Srivastava-Pandey EOS consistently performs well for all the samples compared to other EOS. In conclusion, the Srivastava-Pandey EOS is recommended for accurate pressure calculations. In analyzing NaF, it's evident that most equations of state match experimental values at pressures below 14 GPa. However, above this pressure, all equations of state, except for the Vinet EOS and Srivastava-Pandey EOS, deviate from experimental values. Similar observations were made for NaCl. When examining NaBr and NaI at higher pressures, the Vinet EOS also deviates from experimental results, while the Srivastava-Pandey EOS remains consistent and very close to the experimental values. The reliability of the Srivastava-Pandey EOS is due to its third-order approximation of lattice potential energy, which captures the vibrational behavior of lattice parameters. This sets it apart from other equations of state, which use a second-order approximation. The third-order approximation includes higher degree approximations to account for changes in the material's behavior under compression at atomic and molecular levels. Therefore, the consistent Srivastava-Pandey EOS can be used to predict the compression behavior of halides, for which experimental results are still pending.
| Element | V/V0 | P(V) | P(M) | P(H) | P(B) | P(B-M) | P(S-P) | P(Exp.) |
|---|---|---|---|---|---|---|---|---|
| NaF | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.924 | 4.5 | 4.6 | 4.5 | 4.5 | 4.5 | 4.5 | 4.4 | |
| 0.868 | 9.5 | 9.8 | 9.5 | 9.6 | 9.6 | 9.5 | 9.4 | |
| 0.827 | 14.4 | 15.2 | 14.5 | 14.7 | 15 | 14.5 | 14 | |
| 0.803 | 17.9 | 19.2 | 18 | 18.5 | 18 | 18 | 17 | |
| 0.8 | 18.4 | 19.8 | 18.5 | 19 | 19 | 18.5 | 18 | |
| 0.777 | 22.3 | 24.6 | 22.6 | 23.3 | 23 | 22.6 | 21 | |
| 0.774 | 22.9 | 25.3 | 23.2 | 23.9 | 23 | 23.1 | 22 | |
| 0.758 | 26.1 | 29.2 | 26.4 | 27.4 | 27 | 26.4 | 25 | |
| 0.743 | 29.4 | 33.5 | 29.8 | 31 | 30 | 29.7 | 29 | |
| NaCl | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.904 | 3.2 | 3.2 | 3.2 | 3.2 | 3.2 | 3.1 | 3 | |
| 0.76 | 13.4 | 15.1 | 13.6 | 14.1 | 14 | 13.5 | 12 | |
| 0.702 | 21.1 | 25.5 | 21.5 | 22.9 | 22 | 21.3 | 20 | |
| 0.699 | 21.6 | 26.2 | 22 | 23.5 | 23 | 21.8 | 21 | |
| 0.697 | 21.9 | 26.7 | 22.4 | 23.9 | 23 | 22.1 | 22 | |
| 0.675 | 25.8 | 32.6 | 26.4 | 28.5 | 27 | 26.1 | 25 | |
| 0.658 | 29.2 | 38 | 30 | 32.7 | 31 | 29.6 | 29 | |
| 0.636 | 34.3 | 46.6 | 35.4 | 39.1 | 37 | 34.7 | 34 | |
| 0.628 | 36.3 | 50.2 | 37.6 | 41.8 | 39 | 36.8 | 37 | |
| NaBr | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.901 | 2.8 | 2.8 | 2.8 | 2.8 | 2.8 | 2.8 | 2.6 | |
| 0.741 | 13.2 | 15.2 | 13.3 | 14 | 14 | 14 | 13 | |
| 0.725 | 14.9 | 17.6 | 15.2 | 16 | 15 | 15.9 | 16 | |
| 0.663 | 23.8 | 31 | 24.5 | 26.7 | 25 | 25.9 | 26 | |
| 0.638 | 28.6 | 39.1 | 29.5 | 32.8 | 31 | 31.4 | 30 | |
| 0.622 | 32.1 | 45.5 | 33.3 | 37.5 | 35 | 35.4 | 36 | |
| 0.61 | 35.1 | 51.1 | 36.5 | 41.4 | 38 | 38.8 | 39 | |
| NaI | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0.874 | 2.9 | 3.1 | 3 | 3 | 3 | 2.9 | 2.7 | |
| 0.853 | 3.7 | 3.9 | 3.7 | 3.8 | 3.7 | 3.8 | 3.8 | |
| 0.839 | 4.3 | 4.5 | 4.3 | 4.4 | 4.3 | 4.3 | 4.4 | |
| 0.758 | 8.8 | 10 | 8.9 | 9.3 | 9.1 | 8.9 | 8.7 | |
| 0.694 | 14.6 | 18.1 | 14.9 | 16 | 15 | 14.9 | 15 | |
| 0.648 | 20.6 | 27.8 | 21.2 | 23.5 | 22 | 21.1 | 21 | |
| 0.609 | 27.4 | 40.5 | 28.5 | 32.6 | 30 | 28.2 | 28 | |
| 0.579 | 34.2 | 54.6 | 35.8 | 42.2 | 38 | 35.2 | 36 |
Table 2: Values of P (GPA) calculated from Vinet EOS P(V), Murnaghan EOS P(M), Holzapfel EOS P(H), Born-Mie EOS (B), Birch-Murnaghan EOS P(B-M) and Srivastava-Pandey P(S-P).
Conclusion
The study found that the Vinet EOS and Srivastava-Pandey EOS can calculate the pressure at various compression levels. Both methods agree with experimental results at low pressures (≤ 14GPa). However, the Vinet EOS deviates from experimental results at higher compression levels, whereas the Srivastava-Pandey EOS provides pressure values that closely align with experimental data. Therefore, the Srivastava-Pandey EOS is the most accurate method for predicting pressure at high halide compression levels. The accuracy of the Srivastava-Pandey EOS increases with compression order.
Ethical Approval
The authors confirm that the manuscript is original and unpublished.
Competing Interests
The authors of this paper declare no known financial interests or personal relationships that could have affected the presented work.
Author's Contribution
All the authors collaborated to create the research outline. Abhay P. Srivastava performed all the necessary calculations and drafted the initial manuscript. Professor B. K. Pandey provided resources and guidance throughout the project, while Dr. Narendra Prasad Tripathi and Dr. Mukesh Upadhyaya gave valuable suggestions and advice.
Funding
The authors have clarified that they do not have any funding agency available for their work.
References
- Zhou M, Zhu W, Yu S, et al. Composites Part C: Open Access. 2022; 7: p. 100212.
- Liang W, Jia J, Lv J, et al. Chemical Phy Letters. 2015; 622: p. 57-62.
- Abbaspour M, Akbarzadeh H, Salemi S, et al. Physica A: Stat Mech App. 2016; 462: p. 1075-1090.
- Long X, Bai Y, Algarni M, et al. Mat Sci Eng. 2015; 645: p. 347-356.
- Duan B, Zhou Y, Wang D, et al. J Alloys Compd. 2019; 771: p. 498-504.
- Chen J, Yan L, Liang S, et al. J Alloys Compd. 2022; 901: p. 163-1744.
- Cho S, Jo I, Jung BM, et al. Scr Mater. 2017; 136: p. 50-54.
- Jagannatham M, Sankaran S, Haridoss P. Mat Sci Eng. 2015; 638: p. 197-207.
- Nandanwar CM, Kokode NS, Yerojwar RM, et al. Nano Struc Nano Obj. 2023; 36: p. 101-168.
[Crossref]
- Zhong M, Zhang M, Li X. Carb Ener. 2022; 4(5): p. 950-985.
[Crossref]