Research Article - Der Pharma Chemica ( 2018) Volume 10, Issue 5
Impact of Dielectric Constant on Binary Complexes of Ca(II), Zn(II) and Mn(II) Ions with L-proline
Boddu Veeraswami1* and Gollapalli Nageswara Rao2
1GITAM Institute of Technology, GITAM University, Visakhapatnam-530045, India
2School of Chemistry, Andhra University, Visakhapatnam-530003, India
- *Corresponding Author:
- Boddu Veeraswami
GITAM Institute of Technology
GITAM University
Visakhapatnam-530045, India
Abstract
Binary complexes of Ca(II), Zn(II) and Mn(II) with L-proline was investigated pH-metrically in 1,2-propanediol-water mixtures by maintaining an ionic strength of 0.16 mol.L-1 at 303.0 K. The best-fit chemical models for present study are ML+, MLH2+ and ML2H+ for Ca(II), Zn(II) and Mn(II) ions are established from modelling studies using computer program MINIQUAD75. Some errors influence the magnitudes of stability constants and its order is alkali > acid > ligand > metal. The graphical representation of log β against 1/D of the medium shows that dominance of electrostatic interactions. Distribution diagrams of the various species of the binary complexes in relation to pH at different variations (0.0-60.0% v/v) of propylene glycol-water mixtures were presented.
Keywords
Binary complexes, MINIQUAD75, Stability constant, Propylene glycol
Introduction
The binary complexes of Ca(II), Zn(II) and Mn(II) with L-proline are studied in the presence of propylene glycol (PG) to understand the influence of co-solvent on the chemical speciation studies. A number of studies have been reported on chemical speciation of α-amino acids in different media in recent times [1-3]. Chemical speciation of a molecule is depends on its structure and dielectric constant of the medium [4,5]. L-Proline is one of the twenty deoxyribonucleic acid encoded amino acids [6,7]. It contains pyrrole type nitrogen rather than the amino nitrogen of the amino acids [8,9]. Proline derivatives are used as asymmetric catalysts in organic reactions, like the Corey-Bakshi-Shibata (CBS) reduction [10] and aldol-condensation [11]. Cyclomonomer formation in penta and hexapeptides [12] was drastically hindered by the presence of proline regardless of position.
Calcium plays an important role in cell membranes and as a structural component. It helps in blood clotting, improving bone density, nerve signaling and muscle contraction and relaxation [13]. Lack of calcium leads to rickets and osteoporosis, osteonecrosis, hypertension and other disorders. The present research [14,15] showed that vitamin D is needed to absorb calcium. Zinc is another abundant essential trace metal after iron and it plays vital role in bio-systems [16-19]. It supports normal growth and development during pregnancy, childhood and adolescence and is required for proper sense of taste and smell [20-22].
Manganese is a trace nutrient its deficiency caused skeletal deformities [23] and it is bound to manganese metalloproteins, mostly glutamine synthetase in astrocytes [24] in humans. 1, 2-Propanediol (or) Propylene glycol (PG) is an organic compound and it acts as a solvent in many pharmaceuticals applications [25]. Propylene glycol is metabolized in the human body into pyruvic acid, acetic acid and lactic acid [26], and a highly toxic substance, propionaldehyde [27]. Propylene glycol also acts as a mild anesthetic/CNS-depressant [28].
Experimental Section
Materials and methods
0.05 mol.L-1 solutions of L-proline (SRL, India) and to increase the solubility of 0.1 mol.L-1 solutions of metal (Ca, Zn & Mn) chlorides (GR, E-Merck, Germany) by 0.05 mol.L-1 of HCl in triple distilled water. Propylene glycol (Qualigens, India) was used without further purification. 0.4 mol.L-1 carbonate free sodium hydroxide (Qualigens, India) and 0.2 mol.L-1 hydrochloric acid (Qualigens, India) solutions were used. 2.0 mol.L-1 solution of sodium chloride (Qualigens, India) were prepared to maintain 0.16 mol.L-1 ionic strength in the titrant. The strengths of acid and alkali were investigated by Gran plot method [29,30] and these data analyses for variance of one way classification ANOVA [31,32].
Systronics MK-VI digital pH meter is used for alkali metric titrations at different composition of propylene glycol (0.0-60.0% v/v) with an ionic strength 0.16 mol L-1 of NaCl at 303.0 K. The quantity of L-proline in the titrands is 0.250, 0.375 and 0.500 mmols.
Modeling method
The simulated acid-base titrations data (pH Ci) calculated by SCPHD [33] programs were used to compute correction factor (log F) for each of the solvent compositions. For binary metal complexes, the approximate stability constants were obtained from MINIQUAD75 program [34] by graphical interpolation of formation curve for ML (metal-ligand) type complexes. In the present investigation, the author has obtained the data from linear least squares analysis of the pruned formation data and graphical method.
Results and Discussion
The results of the best fit chemical species of Ca(II), Zn(II) and Mn(II) with L-proline in propylene glycol-water mixtures and their overall formation constants are given in Table 1. Which are supported by the low standard deviation (SD) in log β and the small values of Ucorr represent by this model.
| %v/v PG |
log βmlh (SD) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ML+ | MLH2+ | ML2H+ | NP | *Ucorr | Skew ness |
χ2 | Kurtosis | R- factor |
pH range |
||||
| Ca (II) | |||||||||||||
| 0 | 2.18 (65) | 12.66 (63) | 15.06 (35) | 25 | 2.86 | 1.44 | 36.89 | 5.61 | 0.0153 | 2.8-10.8 | |||
| 10 | 2.27 (43) | 12.93 (12) | 15.44 (36) | 66 | 2.71 | 0.31 | 79.17 | 4.08 | 0.0449 | 2.3-11.0 | |||
| 20 | 3.59 (18) | 12.97 (16) | 15.86 (47) | 80 | 4.62 | 1.57 | 94.4 | 9.31 | 0.0097 | 1.7-11.0 | |||
| 30 | 3.47 (16) | 13.00 (8) | 16.50 (31) | 38 | 12.63 | 0.96 | 50.49 | 9.43 | 0.0057 | 1.5-11.0 | |||
| 40 | 2.27 (11) | 13.13 (10) | 15.43 (72) | 41 | 13.92 | 0.73 | 26.53 | 2.61 | 0.0243 | 1.9-11.0 | |||
| 50 | 3.04 (10) | 12.97 (6) | 15.70 (69) | 45 | 1.12 | 0.6 | 29.09 | 5.88 | 0.0045 | 1.5-11.0 | |||
| 60 | 2.54 (13) | 12.44 (14) | 15.19 (55) | 50 | 1.84 | 1.08 | 60.13 | 7.39 | 0.005 | 1.6-11.0 | |||
| Zn (II) | |||||||||||||
| 0 | 6.77 (48) | 13.25 (11) | 20.30 (50) | 38 | 3.66 | 0.32 | 35.19 | 8.1 | 0.0098 | 1.6-8.9 | |||
| 10 | 6.40 (40) | 12.52 (18) | 19.37 (29) | 82 | 9.01 | 0.88 | 128 | 10.81 | 0.0141 | 1.5-9.4 | |||
| 20 | 6.59 (32) | 13.74 (12) | 19.70 (48) | 39 | 5.81 | 0.44 | 30.76 | 5.02 | 0.013 | 1.5-9.4 | |||
| 30 | 6.64 (48) | 13.35 (12) | 20.22 (60) | 40 | 5.73 | 0.36 | 43.47 | 7.08 | 0.0122 | 1.5-9.4 | |||
| 40 | 6.99 (33) | 13.93 (8) | 20.33 (67) | 84 | 5.76 | 0.77 | 100.3 | 8.86 | 0.0111 | 1.5-9.4 | |||
| 50 | 7.43 (41) | 14.14 (17) | 20.06 (64) | 41 | 11.51 | 0.71 | 27.44 | 6.2 | 0.0174 | 1.5-9.4 | |||
| 60 | 7.09 (41) | 13.85 (13) | 19.50 (46) | 46 | 6.77 | 0.94 | 103.1 | 8.69 | 0.0093 | 1.5-9.4 | |||
| Mn (II) | |||||||||||||
| 0 | 4.05 (31) | 12.38 (9) | 16.79 (23) | 44 | 1.1 | 0.68 | 35.03 | 5.68 | 0.0037 | 1.5-9.8 | |||
| 10 | 4.85 (27) | 12.58 (17) | 17.70 (67) | 42 | 3.42 | 0.92 | 44.92 | 7.88 | 0.0096 | 1.6-9.8 | |||
| 20 | 5.14 (38) | 13.50 (9) | 17.92 (53) | 85 | 5.15 | 0.53 | 84.92 | 7.25 | 0.0094 | 1.6-9.8 | |||
| 30 | 5.37 (29) | 13.76 (11) | 17.61 (26) | 46 | 18.68 | 1.04 | 66.99 | 13.36 | 0.0049 | 1.6-9.8 | |||
| 40 | 5.95 (32) | 13.08 (6) | 18.23 (35) | 90 | 2.97 | 0.94 | 104.9 | 8.3 | 0.0067 | 1.6-9.8 | |||
| 50 | 6.62 (28) | 13.77 (8) | 18.95 (81) | 84 | 4.1 | 0.99 | 77.9 | 9.33 | 0.0094 | 1.5-9.8 | |||
| 60 | 6.10 (70) | 14.31 (19) | 19.84 (72) | 38 | 8.11 | 0.55 | 68.74 | 2.45 | 0.0143 | 1.6-9.8 | |||
*Ucorr=U/(NP-m) × 108;
Where, m=Number of species; NP=Number of experimental points
Table 1: Parameters of best fit chemical models of L-proline complexes of Ca(II), Zn(II) and Mn(II) in PG-water mixtures
Kurtosis and Skewness
If a chemical model is an ideal normal distribution its numerical values are 3 and 0 respectively for kurtosis and skewness. The kurtosis values indicate that the residuals form leptokurtic and very few are in platykurtic patterns [35] from the Table 1. The skewness values are in between 0.31 to 1.57 and low crystallographic R-values shows the residuals form a part of normal distribution, then least squares method can be applied to this data. These statistics shows that the best fit models portray of the metal-L-proline species in PG-water mixtures.
Incorporation of errors
The stability constants (log β) should be changed with respect to the strength of alkali, mineral acid, ligand and metal, which are called as errors. The best fit chemical species evaluation by study of incorporation of errors in Mn(II) –L-proline complexes in 30% v/v of PG-water mixtures on the magnitudes of stability constants. Its order is alkali > acid > ligand > metal. While refinement few (ML) species were rejected with increased SD confirm the influence of ingredients on stability constants and the best fit models shown in Table 2.
| log β (SD) | ||||
|---|---|---|---|---|
| Ingredient | % Error | ML+ | MLH2+ | ML2H+ |
| 0 | 4.05 (31) | 12.38 (9) | 16.79 (23) | |
| -5 | Rejected | Rejected | Rejected | |
| Alkali | -2 | Rejected | 13.40 (14) | 17.61 (39) |
| 2 | 9.49 (66) | 14.43 (55) | 17.61 (39) | |
| 5 | 19.87 (**) | 26.24 (**) | 17.61 (39) | |
| -5 | 21.16 (**) | 27.04 (**) | 17.61 (39) | |
| Acid | -2 | 13.78 (**) | 21.27 (**) | 17.61 (39) |
| 2 | Rejected | 12.37 (26) | 17.61 (39) | |
| 5 | Rejected | Rejected | Rejected | |
| -5 | 4.97 (48) | 13.13 (8) | 17.61 (39) | |
| Ligand | -2 | 5.15 (35) | 13.49 (9) | 17.61 (39) |
| 2 | 5.74 (30) | 14.17 (20) | 17.61 (39) | |
| 5 | 12.43 (**) | 20.89 (**) | 17.61 (39) | |
| -5 | 5.55 (32) | 13.87 (14) | 17.61 (39) | |
| Metal | -2 | 5.44 (30) | 13.80 (12) | 17.61 (39) |
| 2 | 5.30 (29) | 13.73 (10) | 17.61 (39) | |
| 5 | 5.20 (28) | 13.68 (9) | 17.61 (39) | |
Table 2: Effect of errors in influential parameters on the stability constants of Mn(II)-proline complexes in 30% v/v of PG-water mixtures
Solvent effect
Co-solvent influences the protonation and deprotonation equilibria in solution by changing the dielectric constant of the medium, which varies the relative contributions of electrostatic and non-electrostatic interactions. So the variation of the step-wise stability constant in the medium or change in free energy (ΔG) with content depends upon electrostatic and non-electrostatic factors and can be represented as the sum of the changes in free energy due to these two factors.
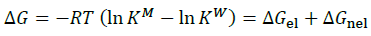 (1)
(1)
KW and KM are the step-wise stability constants in aqueous and in aqua-organic mixture. According to Born’s classical theory [36], the electrostatic forces to the free energy changes (ΔGel) with rigid sphere of radius (r) and dielectric constant (Ds) is as follows.
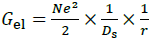 (2)
(2)
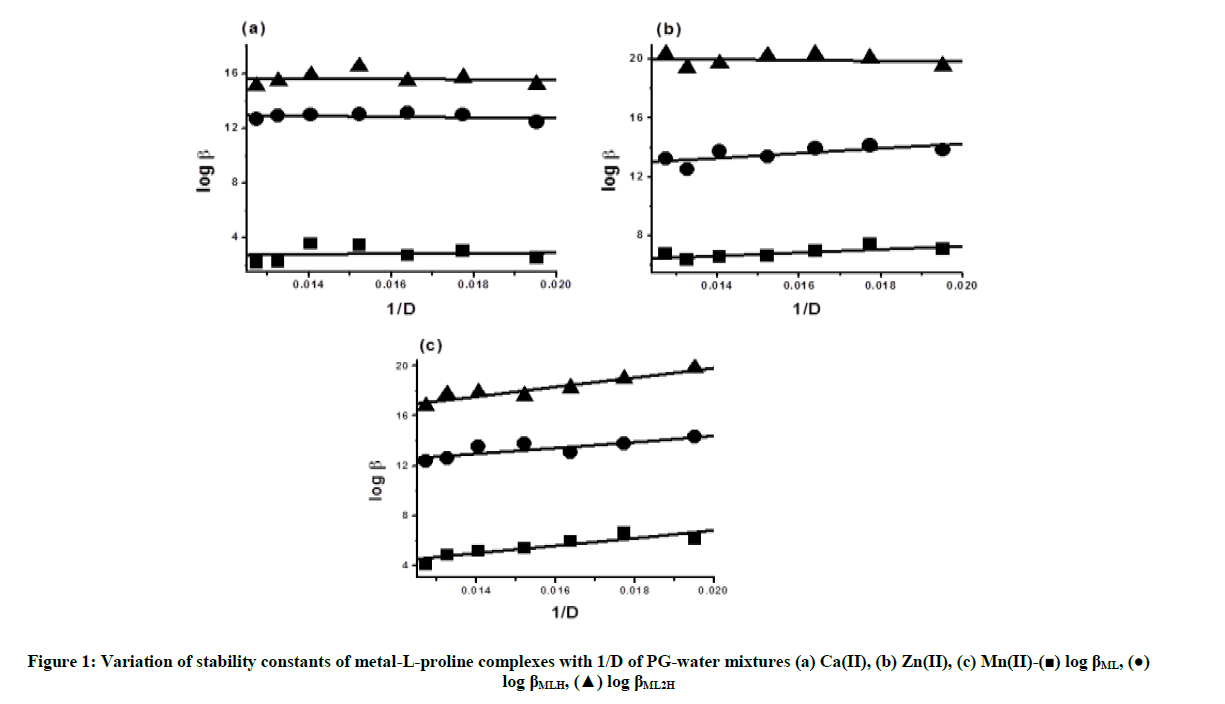
From Equitation 1 and 2, we can say that a plot of log KM versus 1/D should be linear indicates that the electrostatic forces are responsible for the stability trend. The linear variation (Figure 1) indicates that electrostatic forces are dominating the non-electrostatic forces [37,38] in the PG-water mixtures.
Distribution diagrams
L-proline exists as LH2+, LH and L- respectively in the pH-ranges 2.5-4.0, 4.0-10.0 and 10.0-11.0. The binary metal complexes refined are ML+, MLH2+ and ML2H+ for Ca(II), Zn(II) and Mn(II) in PG-water mixtures. The formations of various binary complex species are shown in the following equilibrium.
M + LH2+ ⇌ MLH2+ + H+ (1)
MLH2+ ⇌ ML+ + H+ (2)
M + LH ⇌ ML++ H+ (3)
MLH2+ + LH ⇌ ML2H+ + H+ (4)
ML+ + LH2+ ⇌ ML2H+ + H+ (5)
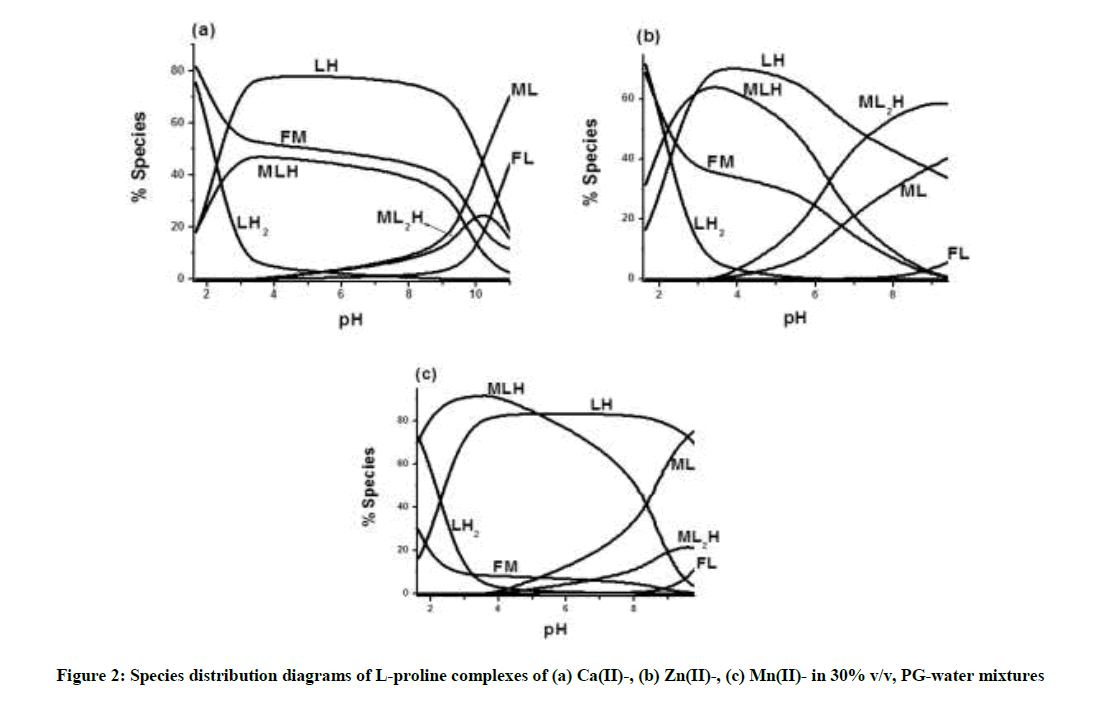
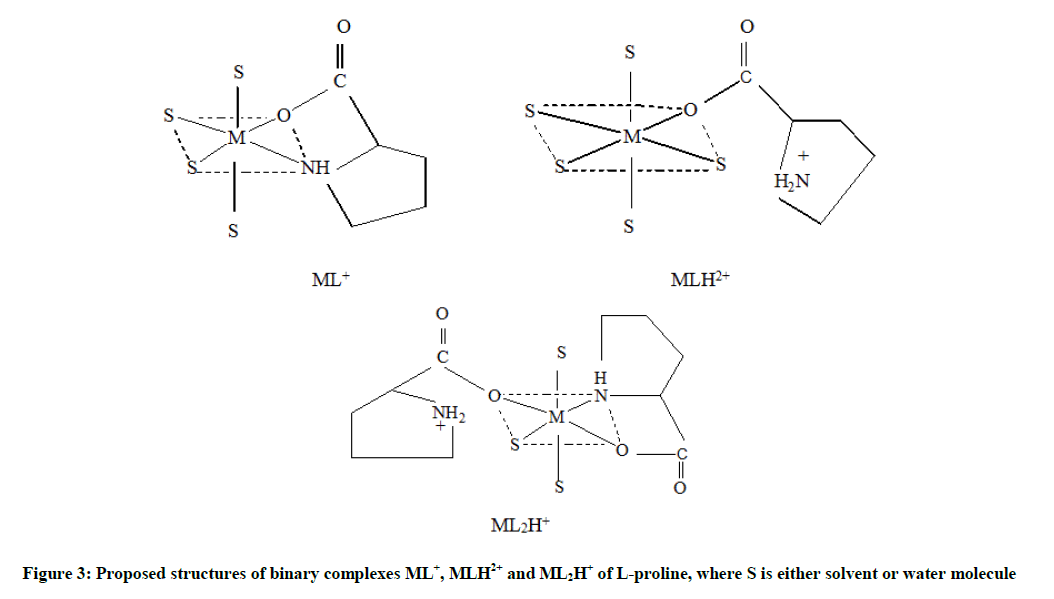
Typical species distribution diagrams are shown in Figure 2, which indicates that the percentages of ML+, MLH2+ and ML2H+ species of Ca(II), Zn(II) and Mn(II) are formed to an extent of 49-92% of ML+ species, 47-92% of MLH2+ species and 24-60% of ML2H+ species are formed in 30% v/v PG-water mixtures. The species ML+, MLH2+ and ML2H+ are formed in the pH range 1.5-11.0. At pH 3.0 MLH2+ species is formed for Ca(II), Mn(II) and Zn(II) (Figure 2) (Equilibrium 1). With increasing pH, MLH2+ is deprotonated to ML+ (Equilibria 2 and 3), at higher pH, ML2H+ is formed (Equilibria 4 and 5). The order of the formation constant is Zn > Mn > Ca, which follows Mellor-Maley's order [39,40]. Under the present experimental conditions the possible structures of metal- L-proline complexes of are given in Figure 3.
Conclusions
Chemical speciation studies of binary complexes of Ca(II), Zn(II) and Mn(II), with L-proline in propylene-glycol-water mixtures are as follows.
• The binary species of L-proline complexes detected are CaL, CaLH, CaL2H, ZnL, ZnLH, ZnL2H, MnL, MnLH and MnL2H in PG-water mixture. These species are validated by statistical treatment of data.
• The binary stability constants (log β) are increased linearly with decreasing dielectric constant of PG resulting electrostatic forces are dominated.
• The order of the ingredients that influence the magnitudes of stability constants due to incorporation of errors is Alkali > Acid > Ligand > Metal.
References
- P.S. Rao, B. Srikanth, V.S. Rao, C.K. Sastry, G.N. Rao, E-J. Chem., 2009, 6, 561.
- M.P. Latha, V.M. Rao, T.S. Rao, G.N. Rao, Bull. Chem. Soc. Ethiop., 2007, 21, 363.
- A. Sharma, K.D. Gupta, K.K. Saxena, J. Indian Counc. Chem., 2002, 19, 43.
- R.W. Taft, Progress in Physical Organic Chemistry, John Wiley & Sons, New York, 1983.
- J. Hens, Structural effects on equilibria in organic chemistry, Wiley, New York, 1975.
- P. Furst, P. Stehle, J. Nutr., 2004, 134, 1558S.
- P.J. Reeds, J. Nutr., 2000, 130, 1835S.
- H.G. Busse, G. Maass, Z. Phys. Chem., 1969, 66, 92.
- H.N. Christensen, A.A. Greene, D.K. Kakuda, C.L. Macleod, J. Exp. Biol., 1994, 196, 297.
- A. Hirao, S. Itsuno, S. Nakahama, N. Yamazaki, Chem. Commun., 1981, 7, 315.
- L. Benjamin, P. Peter, C. Chris, Org. Lett., 2001, 3, 573.
- K. Jana, E. Angelika, B. Michael, Lett. Pept. Sci., 1998, 5, 129.
- C.M. Weaver, R.P. Heaney, Calcium. In: M.E. Shils, M. Shike, A.C. Ross, B. Caballero, R.J. Cousins, editors, Modern nutrition in health and disease, 10th Edi., Lippincott Williams & Wilkins, M.D. Baltimore, 2006.
- G. Bihl, A. Meyers, The Lancet., 2001, 358, 651.
- W.D. Hall, M. Pettinger, A. Oberman, N.B. Watts, K.C. Johnson, E.D. Paskett, M.C. Limacher, J. Hays, Am. J. Med. Sci., 2001, 322, 12.
- E.H. Cox, G.L. McLendon, Curr. Opin. Chem. Biol., 2000, 4, 162.
- J.H. Laity, B.M. Lee, P.E. Wright, Curr. Opin. Struc. Biol., 2001, 11, 39.
- T. Dudev, C.J. Lim, J. Chin. Chem. Soc., 2003, 50, 1093.
- Y.L. Lin, C. Lim, J. Am. Chem. Soc., 2004, 126, 2602.
- A.S. Prasad, F.W. Beck, S.M. Grabowski, J. Kaplan, R.H. Mathog, Proc. Am. Assoc. Physicians., 1997, 109, 68.
- B.L. Vallee, K.H. Falchuk, Physiol. Rev., 1993, 73, 79.
- D.S. Auld, Biometals., 2001, 14, 271.
- J. Emsley, Nature's Building Blocks: An A-Z Guide to the Elements, Oxford, UK: Oxford University Press, 2001.
- A. Takeda, Brain Res. Rev., 2003, 41, 79.
- A. Chauvel, G. Lefebvre, Petrochemical Processes, Editions Technip, 2, 1989.
- D.J. Hamilton, The Lancet., 1890, 2, 306.
- J.A. Ruddick, Toxicol. Appl. Pharmacol., 1972, 21, 102.
- M.A. Seidenfeld, P.J. Hanzlik, J. Pharmacol. Exp. Ther., 1932, 44, 109.
- G. Gran, Analyst., 1952, 77, 661.
- G. Gran, Anal. Chim. Acta., 1988, 206, 111.
- R.S. Rao, G.N. Rao, Computer Applications in Chemistry, Himalaya Publishing House, Mumbai, India, 2005.
- N. Padmaja, M.S. Babu, G.N. Rao, R.S. Rao, K.V. Ramana, Polyhedron., 1990, 9, 2497.
- G.N. Rao, Complex equilibria of some biologically important metal ions in aqua- organic media, PhD thesis, Andhra University, Visakhapatnam, India, 1989.
- P. Gans, A. Sabatini, A. Vacca, Inorg. Chim. Acta., 1976, 18, 237.
- M.P. Latha, V.M. Rao, T.S. Rao, G.N. Rao, Acta. Chim. Slov., 2007, 54, 160.
- M. Born, Z. Phys., 1920, 1, 45.
- A.K. Singh, D.A. Manjula, J. Indian. Chem. Soc., 2001, 78, 635.
- E.H. Cordes, Pure Appl. Chem., 1978, 50, 617.
- D.P. Mellor, L. Maley, Nature., 1947, 159, 370.
- D.P. Mellor, L. Maley, Nature., 1948, 161, 436.