Research Article - Der Pharma Chemica ( 2018) Volume 10, Issue 2
Determination of Pitzer Parameters from Experimental Isotherm of a Ternary System Using Nelder Mead Method
Bouchra Mekkaoui*, Mohamed Jouaiti, Ahmed Jouaiti and Latifa Laallam
Sustainable Development Laboratory, Faculty of Sciences and Techniques, Sultan Moulay Slimane University, Beni-Mellal-23000, Morocco
- *Corresponding Author:
- Bouchra Mekkaoui
Sustainable Development Laboratory
Faculty of Sciences and Techniques
Sultan Moulay Slimane University
Beni-Mellal-23000, Morocco
Abstract
Models have been developed allowing adequate description of the behavior of concentrated aqueous solutions. One of them is the well-known Pitzer model proposed for the description of the properties of dense electrolyte solutions in a wide range of temperatures, pressures, and compositions, thus this one requires the knowledge of interaction parameters between particles. Indeed, Pitzer (1973) has developed its model for an electrolyte while introducing a set of interaction parameters whether binary or ternary ones. Hence, the aim of our work is the numerical determination of theses parameters. We have developed an algorithm based on Pitzer equations as well as the Nelder-Mead simplex method, which is an optimization method for multivariate functions, afterward the algorithm has been approved by applying it on the ternary system, of which we already dispose Pitzer parameters as well as its isotherm, we made use of the ternary system Li2SO4+MgSO4+H2O at 208.15°K, this comparison has successfully confirmed the accuracy and the effectiveness of our work.
Keywords
Phase diagram, Pitzer, Simplex, Equilibrium
Introduction
Solubility equilibrium between solid salts, salt hydrates and water play an important role in different branches of applied chemistry such as, hydrometallurgy, geochemistry and oceanography [1-3]. The large uses and the important applications of solid salts, make the exact knowledge of their physical, chemical and thermodynamic properties requires constantly new investigations, on both of experimental level and numerical one. Hence, the development of a thermodynamic model appears necessary in order to predict, from the initial composition of the solution, its properties, its behaviour (In the case of a change temperature, pressure).
Models can be powerful predictive and interpretive tools to study the geochemistry of natural waters and mineral deposits, solve environmental problems and optimize industrial processes; indeed the Pitzer model is one of the most used ones, which has enjoyed remarkable success. It is especially popular with geochemists, waste chemists, and engineers for prediction of mineral solubility and phase equilibrium. Therefore, Pitzer and his co-workers developed the ion-interaction approach to predict the mean activity coefficients of salts in aqueous electrolyte solutions as a function of the molality as well as the theoretical solubility isotherms [4-6]. Furthermore it’s used for thermodynamic analysis of the experimental mixing solutions solubility data, presented in the literature. Pitzer has determined the ion interaction parameters for a large number of binary and ternary solutions [7]. The specific interaction approach for describing aqueous solutions to high concentration represents a significant advance in physical chemistry that has facilitated the construction of accurate thermodynamic models. However, when the Pitzer parameters are not available from experimental data; they can be theoretically or experimentally determined, as well be seen in the present paper.
A several methods have been used for the determination of Pitzer parameters, however some of them are judged expensive in terms of money due to the huge need of materials, energy and equipment; one of the most known processes for Pitzer parameters determination is the isopiestic method [8] which is an experimental method based on the calculation of the osmotic coefficient and water activity, another method has been used recently, that aims to predict Pitzer parameters through the calculation of thermodynamic properties using the hygrometric method [9], in a previous work we opted for an iterative method to estimate Pitzer parameters for a ternary system [10], furthermore to enhance our work, we established an algorithm based essentially on the simplex Nelder-Mead method which is an optimization routine with the main object of searching for the Pitzer parameters while minimizing the difference between experimental data and theoretical one.
Calculation model
The details of ion- interaction have already been discussed in preceding Pitzer publication, the following equation 1, 2 and 3 are the main equations employed in our calculations.
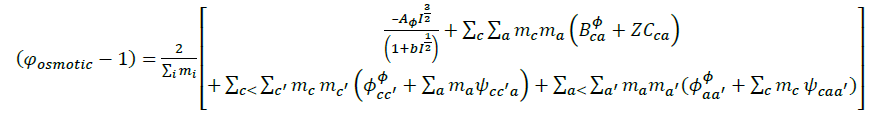 (1)
(1)
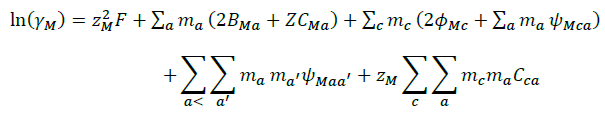 (2)
(2)
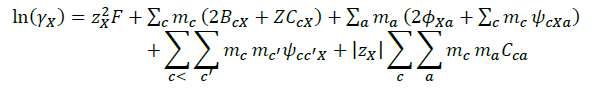 (3)
(3)
The summations in Equations 1, 2 and 3 over c and a respectively are summations over the cations and the anions respectively present in the solution. The various terms in Equations 1, 2 and 3 are defined as follows:
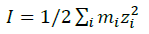 (4)
(4)
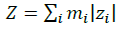 (5)
(5)
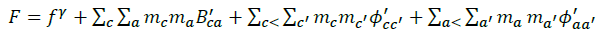 (6)
(6)
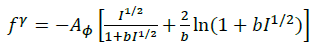 (7)
(7)
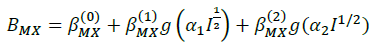 (8)
(8)
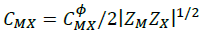 (9)
(9)
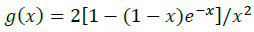 (10)
(10)
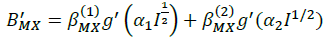 (11)
(11)
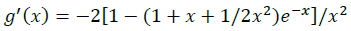 (12)
(12)
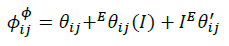 (13)
(13)
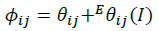 (14)
(14)
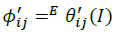 (15)
(15)
The ion-interaction model gives an equation for the activity and osmotic coefficient of electrolyte solution depending to four binary parameters, β(0), β(1), β(2), Cϕ and two ternary ones ψ and θ. These parameters allow us the calculation of the equilibrium constant of each component in the systems at different temperature.
The solubility of hydrated salt in electrolyte solutions can be calculated from thermodynamic equations. For a hydrated salt M(SO4)x,yH2O, the solubility at a given temperature for the dissolution reaction: 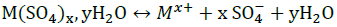 Is given by:
Is given by:
 (16)
(16)
Where, ai and aw represent respectively the activity of the ion i and water.
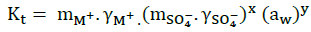 (17)
(17)
Where, mi and γi, represent respectively, the molality and the activity coefficient of the ions . The activity of water is related to the osmotic coefficient [5] by the given Equation:
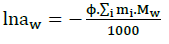 (18)
(18)
In which, Mw: Represents the molecular mass of water, the sum covers all solute spices. Activity and osmotic coefficients are calculated by using the Pitzer model [4-6].
Theoretical model
The object of the algorithm
In this work, we settle for the determination of Pitzer parameters for binary and ternary systems, it will subsequently be a pillar of the next work, in which we will face another algorithm that the mean object is to establish the isotherm of a system, while relying firstly on the mathematical model mentioned before and secondly, on the equilibrium points that it has been found experimentally with a synthetic method based on measurements of the conductivity, this algorithm will be based primarily on the research of molar fraction in condition that the solubility in ternary system is the same in the binary one.
The principle of the algorithm
Our algorithm is based on finding the Pitzer parameters for a system that we know the experimental data. The principle is to change the values of these parameters in order to minimize the objective function, indeed this function is expressed in terms of the gap between experimental and theoretical values calculated from the Pitzer parameters at each iteration.
To do so, we made use of the Nelder-Mead simplex method [11] which is an optimization routine that works with irregular objective functions. In our case we have a function of 10 parameters, so it compares the objective function at the 11th vertices of a simplex and updates the worst vertex through simplex search steps. This method consist in getting a set of operations linked in a closed loop that stops when the gap between experimental and theoretical values calculated from the Pitzer parameters, is infinitesimal, a brief explanation of these operations is subsequently introduced.
Initialization: we initialize the programs by a set of vectors chosen such that they are not collinear.
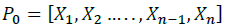
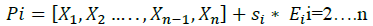
Where, Ei = [e1,e2,... .. ej, ... ... en] is a vector of size n-1, with, ej=1 if i=j otherwise ej=0.
Si is an added step to each parameter of the vector, in order to create n+1 initial vector, the Si value is chosen such that each parameter Xi is always between two reasonable values previously set by the author.
Order: Order vectors while respecting the ascending order of the objective function values. We suppose:
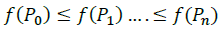
Centroid: for each one of iterations, we compute the centroid from the Equation:
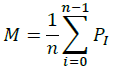
Reflect: This step is based on computing the reflection of the worst vector, in our case it’s 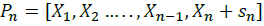 , the reflection vector is calculated using the relation:
, the reflection vector is calculated using the relation:
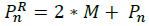
Expand: when we have moved in the correct direction we use the expansion to improve the reflection vector by using the Equation:
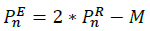
Contract: in case the reflection has no impact on the worst vector that we want to improve, we made use of contraction starting from the relation:
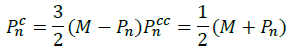
Shrink: shrinkage is a reset vector in case all mentioned operations have not led to the desired result.
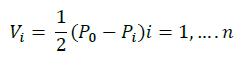
The unordered vertices of the simplex at the next iteration consist of 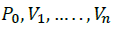
The flowchart
Below the flowchart that generally summarizes all operations mentioned before, while respecting conditions and sequences of the algorithm, since the initialization of starting set of vectors until accurate the correct Pitzer parameter values.
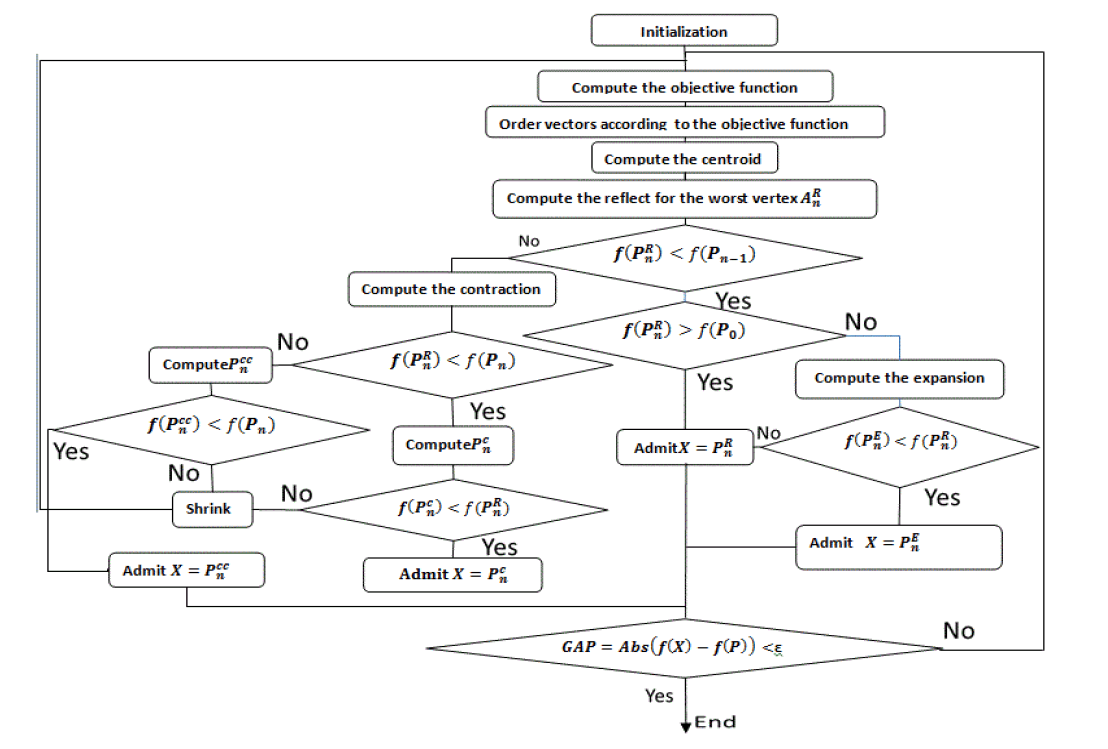
This flowchart summarizes all operations that were mentioned before. We are searching for the minimum of the objective function name df.
The objective function f
It is in terms of the standard deviation between the experimental points and the theoretical function.
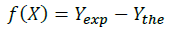
The theoretical function (Ythe)is establishedAfter adjustment of the theoretical points found using the Pitzer model at 35°C, indeed, In order to define the pairs of solubility limits for the ternary system, we made use of an iterative method that consists essentially of equalizing the equilibrium constant of the binary (Kb) and the ternary system (Kt) corresponding to the same solid phase [10].
First, we calculated the equilibrium constant Kb for the binary system for initial Pitzer parameters, then, the equilibrium constant Kt for the ternary system is calculated for the same initial Pitzer parameters while varying the molality of caution and anion, as well as the water quantity.
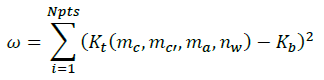
Where, Npts: Number of data points in the solubility isotherm, mc, mc’: Molality of cation, ma: Molality of anion, nw: Water quantity.
The initialization set
The choice of the initializing set vector influences the algorithm execution, in terms of time and convergence towards the desired result, thus we’ve opted for the closest set of vectors to this result, by computing the objective function for multiple sets arbitrarily chosen by the program, in order to increase its precision and minimize its uncertainty, indeed we discovered that the initialization vector has to be chosen such that all parameters belong to limited domains of variation. As indicated in the flowchart, a closed loop will be repeated until the difference between the best and the worst vectors is inferior to a very small value named epsilon (ε).
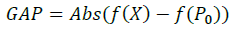
Results and Discussion
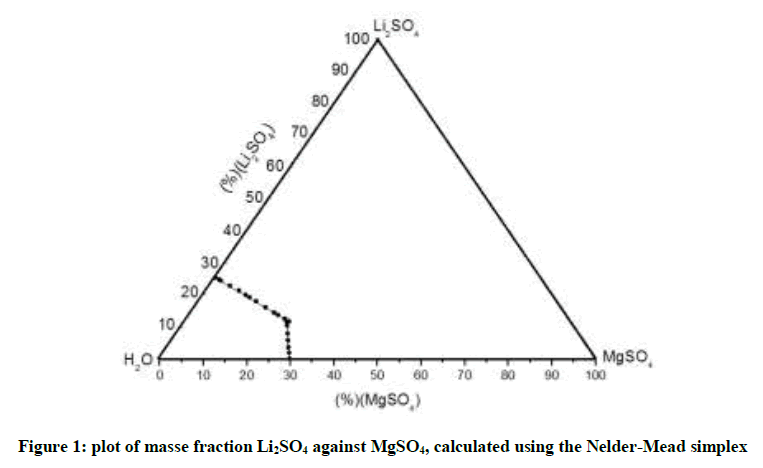
In order to confirm our algorithm elaborated for the Pitzer parameters determination, we opted to apply it on several ternary systems, of which we already know experimental points as well as the parameters of Pitzer. In this paper we’ve chosen to represent Li2SO4 + MgSO4+H2O ternary system. Indeed its isothermal has been established at T=35°C [12]. A comparison was made between the results of our program, and existing data in literature [12-22] as will show tables below.
The Figure 1 below shows the solubility limits calculated from the developed method, it is a triangular representation of the mass fractions. As it’s clearly shown in the curve, the results that we found from the simplex method based on Pitzer calculation model are identical to those of previous works, where they experimentally studied the system behavior in order to establish the isothermal curve [12].
From the Tables 1-3 above, the used method to determine the Pitzer parameters is successful; furthermore, the standard deviation between the literature values and those found from the simplex is relatively small. However It allows to make a quick estimation of the Pitzer parameters, in fact, the choice of the initialization set is wide important for calculation convergence, indeed, we have chosen vectors in contrast to a reasonably limited variation domain, otherwise the program can be lost in calculation, without getting the desired results. Another method strength, that cannot be ignored, is that in the case we know parameters of the first binary system; we can find parameters of the second, as well as ternary ones more precisely, because the number of unknowns in the calculation will be reduced, we deduce that the less parameter we search, the more efficient is the method.
| Salts | β0 | β1 | β2 | Cφ | Reference | |
|---|---|---|---|---|---|---|
| Calculated | Li2SO4 | 0.135 | 1.249 | -0.001 | ||
| Literature | 0.141275 | 1.28459 | -0.0063125 | [13] | ||
| 0.1308 | 1.2913 | -0.000894 | [20] | |||
| 0.136275 | 1.2705 | 0.00399338 | [21] | |||
| 0.1339 | 1.282 | -0.00333 | [22] | |||
| Calculated | MgSO4 | 0.209 | 3.310 | -58.51 | 0.037 | |
| Literature | 0.208097 | 3.5178 | -30.21 | 0.03986 | [13] | |
| 0.2210 | 3.343 | -37.23 | 0.025 | [14,16] | ||
| 0.215 | 3.365 | -32.74 | 0.028 | [17] | ||
| 0.220933 | 3.71015 | -35.2046 | 0.0246099 | [18] | ||
Table 1: single-salts calculated and existing Pitzer ion interaction parameters
| Ternary parameters | θLi,Mg | φLi,Mg,SO4 | Reference |
|---|---|---|---|
| Calculated | -0.117 | 0.037 | |
| literature | -0.0743 | 0.04165 | [19] |
Table 2: Calculated and existing ternary Pitzer ion interaction parameters of Li2SO4+MgSO4+H2O
| Spices | Li2SO4, H2O | MgSO4, 7H2O | References |
|---|---|---|---|
| Calculated (Ks) | 2.302 | 0.015 | |
| Literature (Ks) | 2.8558398 | 0.0266499 0.01634 |
[12] [23] |
Table 3: Comparison of existing and calculated values of the equilibrium constants
Conclusion
The Pitzer model was the basis of the established calculation in this investment, the interaction parameters of Pitzer are determined using the NELDER MEAD method, which is an efficient optimization method in the case of objective functions similar to that studied in the present work. The successful calculations for several ternary systems Pitzer parameters indicate that the method was applicable, and efficient for solutions based on metal salts. The example of the Li2SO4 + MgSO4+H2O ternary system was represented in this paper to confirm our algorithm.
References
- L. Peltier, P. Chaumette, J. Saussey, M.M. Bettahar, J.C. Lavlley, J. Mol. Catal. A Chem., 1998, 132, 91-100.
- A. Monzon, E. Romeo, C. Royo, R. Trujillano, F.M. Labajos, V. Rives, Appl. Catal. A., 1999, 185, 53-63.
- H.G. El-Shobaky, M. Mokhtar, G.A. El-Shobaky, Appl. Catal. A., 1999, 180, 335-344.
- K. Pitzer, J. Phys. Chem., 1973, 77, 268-277.
- K. Pitzer, G. Mayourga, J. Phys. Chem., 1973, 77, 2300-2308.
- K. PitzerM, J.J. Kim, J. Am. Chem. Soc., 1974, 96, 5701-5707.
- https://pubs.usgs.gov/wri/1988/4153/report.pdf
- H. Park, P. Englezos, Fluid Phase Equilibria., 1999, 155(2), 251-259.
- M.E. Guendouzi, A. Dinane, A. Mounir, J. Solution Chem., 2002, 31(2), 119-129.
- A. Jouaiti, B. Mekkaoui, M. Boulghallat, A. Barroug, L. Lâallam, Int. J. Appl. Eng. Res., 2015, 10(20), 41326-41328.
- J.C. Lagarias, J.A. Reeds, M.H. Wright, P.E. Wright, SIAM J Optimization., 1998, 9(1), 112-147.
- S. Wang, T. Deng, J. Chem. Thermodyn., 2008, 40(6), 1007-1011.
- I.N. Lepeshkov, N.N. Romashova, Russ. J. Inorg. Chem., 1960, 5, 2512-2517.
- K.S. Pitzer, J. Phys. Chem., 1973, 77(2), 268-277.
- C.E. Harvie, J.H. Weare, Geochimica et Cosmochimica Acta., 1980, 44(7), 981-997.
- C.E. Harvie, N. Møller, J.H. Weare, Geochimica et Cosmochimica Acta., 1984, 48(4), 723-751.
- J.A. Rard, D.G. Miller, J. Chem. Eng. Data., 1981, 26(1), 33-38.
- R.T. Pabalan, K.S. Pitzer, Geochimica et Cosmochimica Acta., 1987, 51(9), 2429-2443.
- V.K. Filippov, V.I. Nokhrin, Russ. J. Inorg. Chem., 1985, 30, 282-286.
- K.S. Pitzer, Pure Appl. Chem., 1986, 58(12), 1599-1610.
- K.S. Pitzer, G. Mayorga, J. Phys. Chem., 1973, 77(19), 2300-2308.
- H.F. Holmes, R.E. Mesmer, J. Chem. Thermodyn., 1986, 18(3), 263-275.
- L. Meng, D. Li, Brazilian J. Chem. Eng., 2014, 31(1), 251-258.