Research Article - Der Pharma Chemica ( 2024) Volume 16, Issue 5
Ab Initio and Density Functional Theory (DFT) Study on Benzodiazepines
Musa E. Mohamed Babiker1*, Ahmed A. Alzharani1, Ayyob M. Bakry2 and Mohammed B. Hawsawi32Department of Physical Sciences, Chemistry Division College of Science, Jazan University, Jazan, Saudi Arabia
3Department of Chemistry, Umm Al-Qura University, Makkah, Saudi Arabia
Musa E. Mohamed Babiker, Department of Chemistry, Albaha University, Albaha, Saudi Arabia, Email: musa.elballa@gmail.com
Received: 25-Sep-2024, Manuscript No. DPC-24-148781; Editor assigned: 28-Sep-2024, Pre QC No. DPC-24-148781 (PQ); Reviewed: 01-Oct-2024, QC No. DPC-24-148781; Revised: 06-Oct-2024, Manuscript No. DPC-24-148781 (R); Published: 14-Oct-2024, DOI: 10.4172/0975-413X.16.5.469-474
Abstract
Quantum chemical calculations have been carried out to investigate the molecular structure, atomic charge and global reactivity descriptors of benzodiazepines such as EHOMO, ELUMO, ΔE(L-H), ionization potential, electron affinity, electronegativity, molecular hardness, dipole moment and shapes, were determined and used to identify the stability and reactivity of benzodiazepines. The optimized geometry and these parameters were obtained by Ab initio Restricted Hartree Fock (RHF) and Density Functional Theory (DFT) methods in gas phase and in aqueous phase with complete relaxation in the potential energy surface using the 6-31G basis set. Theoretical values are compared with the experimental data.
Keywords
Benzodiazepines; Reactivity descriptors; Ab initio and DFT
Introduction
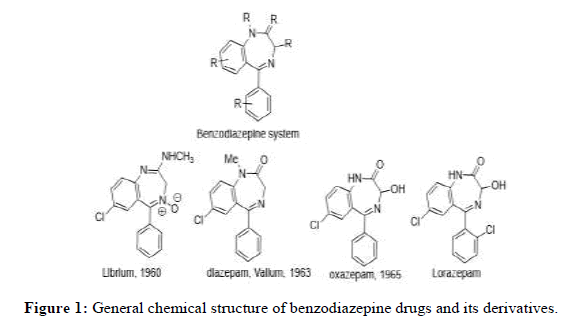
Benzodiazepine is a class of biologically active organic molecules that function as therapeutic agents. They have different derivatives with various pharmaceutical and chemical properties that lead to explore more on their discovery as drugs. They are widely used as tranquilizers and mental health suppressants. They are vital bioactive heterocycle moiety, consist of seven-member ring containing two nitrogen atoms called diazepine. This diazepine ring is fused to a benzene ring. Benzodiazepine has several derivatives that are important as drugs used as anti-anxiety, anticonvulsants and anti-depression, (Figure 1). The biological activity of benzodiazepine compounds tempts the chemists to explore its chemical features and applications [1].
Benzodiazepines are the most prescribed drugs around the world because they have noticeable effects on mental relaxation. Chlorodiazepine [7- chloro-2-(methylamino)-5-phenyl-3H-l,4-benzodiazepine 4-oxide] is the first benzodiazepine derivative successfully synthesized in 1969, and was traded under the name (Librium) [1]. Another traded benzodiazepine is oxazepam patented in 1965 by Wyeth laboratories and later was available in the market under the name Serax [1,2]. In addition, diazepam was discovered to be more power full potent than chlordiazepoxide and was traded under the name of Valium.
Benzodiazepines are pharmacologically active compounds and provide some useful activities such as anxiolytic, sedative-hypnotic anticonvulsant and muscle-relaxant effect [3,4]. We were interested by the molecular properties of these compounds since several publications recently indicated that some benzodiazepine derivatives have been studied because of their biological activity as carcinostatic compounds [5-8] and were highly effective for the relief of anxiety [9-15]. They have a lower potential for addiction than many other drugs that were used earlier and are less likely to cause death or serious, lasting harm when taken in overdoses. The benzodiazepine drugs now use in clinical worldwide, their uses have become less popular because of side effects, including dependence. Different types of benzodiazepine derivatives are now available for prescription and some other similar of this family are still active under clinical evaluation. Lormetazepam is also hypnotic and is another class of a benzodiazepine mostly used for treating insomnia.
Benzodiazepines are pharmacologically active compounds and provide some useful activities such as anxiolytic, sedative-hypnotic, anticonvulsant and muscle-relaxant effect [3,4]. Different types of benzodiazepine derivatives are now available for prescription and some other similar of this family are still active under clinical evaluation. Lormetazepam is also hypnotic and is another class of a benzodiazepine mostly used for treating insomnia. Conformational chemical analysis and electronic properties of 21 benzodiazepines were done by using semiempirical methods and empirical energy [16]. Moreover, it was understood that the chemical structure of a compound and its physical and chemical properties has significant influence on its activity both therapeutic and toxicity. Thermochemical investigations and vibrational spectroscopic studies of 1,4-benzodiazepines using Ab initio and DFT methods were done by S. Muthu, et al., [17]. In this research, we investigate the reliability of RHF and B3LYP theory with 6‐31G basis sets in predicting the structural and electronic properties of these compounds. For this purpose, molecular geometry, atomic charge and molecular orbital indices related to their structural stabilities have been analyzed, for understanding the stability and accuracy of quantum chemical model. In order to confirm our obtained theoretical data, the quantities that contain a richness of information concerning details of the electronic structure and three dimensional structure of the molecule.
Materials and Methods
Computational methods
In the present study ab initio Restricted Hartree Fock (RHF) and Density Functional Theory Methods Study B3LYP (DFT) level of theory calculations were performed on an Intel Pentum (R)1.86 GB personal computer with the Gaussian09 [18] software packages. Molecular geometries of Lormetazepam in the gaseous phase and in solvent (water) were fully optimized at the Density Functional Study (DFT) level and Restricted Hartree Fock (RHF) method using the 6-31G basis set. The structures thus obtained were subjected to vibrational analysis calculations toward their characterization as local minima (all positive force constants). The standard state is 1 atm., which is the default in Gaussian calculations. In addition, the effects of solvents on the structure properties were studied by means of the Self-Consistent Reaction-Field (SCRF) method based on PCM developed by Tomasi and coworkers. It is one of the most widely used approaches. In this model, a solute is considered inside a cavity and the solvent as a structure less medium characterized by some parameters such as its dielectric constant, molar volume and Polarizability. The solvent chose for this studies is polar protic solvent namely water (ε=74.80).
Results and Discussion
Molecular geometry
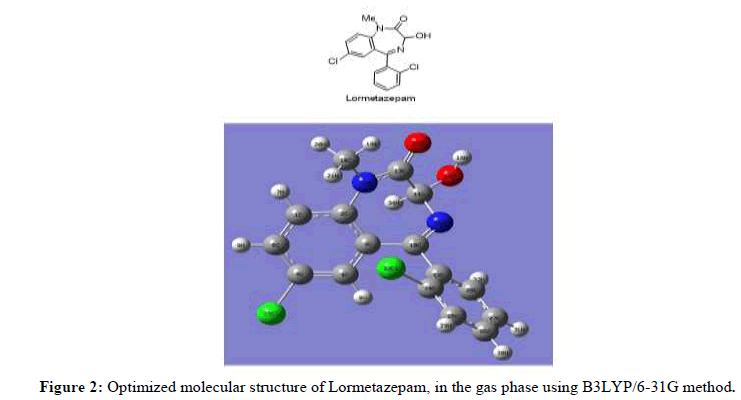
The optimized chemical structure of benzodiazepines analogous, namely Lormetazepam has been illustrated in Figure 2.
The optimized molecular structure for lormetazepam in water and in gas phase were computed by RHF and B3LYP calculations with the 6-31G basis set. The geometrical parameters have been calculated and compared with experimental geometrical parameters of structurally related molecules [19]. The optimized structural parameters obtained from the RHF and B3LYP/6-31G calculations in aqueous phase and the literature values are listed in Table 1, in accordance with the atom numbering scheme given in Figure 2. The slight deviation in literature data from the computed geometry is probably due to the intermolecular interactions in the crystalline state are dominant. A statistical calculation of these data explains that, the bond lengths has been done by B3LYP/6-31G is better than the RHF/6-31G geometry. It can be noted from the correlation coefficient values that the theoretical predictions are in fairly agreement with the experimental value for bond length and bond angles.
Atomic charge
The effective atomic charges calculations serve an important role in quantum mechanical application calculations to molecular systems. The charge distribution on different atoms (C, N, O and Cl) for Lormetazepam. from Mulliken Population Analysis (MPA) procedures using RHF and B3LYP methods is listed in Table 2. From Table 2, it is observed that the calculated Mulliken charge trends are consistent when comparing the RHF and DFT calculations. It is noticed that the carbon atom attached to oxygen and nitrogen atoms (C2, C10, C13 and C14) in both RHF and B3LYP is an electron-deficient atom (i.e., it possesses positive electronic charge). The most negative values are those that are present at nitrogen and oxygen, in the order: N11, N12, O15, O17. The remaining carbon atoms possess negative electronic charge. As the carbon atom C13 is attached with both nitrogen and oxygen in either side, it pulls more charge from C13 atom resulting in more positive charge on the site C13 as compared with that of other carbon atoms. The atomic charges on C3 and C23 atoms become less negative as compared with that other carbon because they are attached to three different carbon atoms [19].
| Bond length | RHF | B3LYP | Exp* | Bond angle | RHF | B3LYP | Exp* |
|---|---|---|---|---|---|---|---|
| C1-C2 | 1.393 | 1.406 | 1.409 | C2-C1-C6 | 120.9 | 121.1 | 120.8 |
| C1-C6 | 1.381 | 1.393 | 1.383 | C1-C2-C3 | 119.5 | 119.5 | 120.9 |
| C2-C3 | 1.4 | 1.419 | 1.418 | C1-C2-N12 | 118.2 | 118 | 116.2 |
| C2-N12 | 1.422 | 1.429 | 1.406 | C3-C2-N12 | 122.2 | 122.3 | 122.7 |
| C3-C4 | 1.396 | 1.41 | 1.403 | C2-C3-C4 | 119.1 | 118.8 | 117.3 |
| C3-C10 | 1.486 | 1.486 | 1.48 | C2-C3-C10 | 121.8 | 122.6 | 122.8 |
| C4-C5 | 1.372 | 1.384 | 1.403 | C4-C3-C10 | 118.9 | 118.5 | 119.8 |
| C5-C6 | 1.381 | 1.393 | 1.377 | C3-C4-C5 | 119.9 | 120 | 120.1 |
| C5-Cl22 | 1.81 | 1.828 | 0 | C4-C5-C6 | 121.6 | 121.8 | 122.7 |
| C10-N11 | 1.268 | 1.296 | 1.289 | C4-C5-Cl22 | 119.8 | 119 | ------ |
| C10-C23 | 1.492 | 1.494 | 1.494 | C1-C6-C5 | 118.8 | 118.5 | 118 |
| N11-C14 | 1.453 | 1.469 | 1.46 | C3-C10-N11 | 123.2 | 123.9 | 125.3 |
| N12-C13 | 1.349 | 1.367 | 1.371 | C3-C10-C23 | 119.2 | 119.2 | 118.5 |
| N12-C18 | 1.474 | 1.483 | ----- | N11-C10-C23 | 117.4 | 116.6 | 116.2 |
| C13-C14 | 1.521 | 1.533 | 1.513 | C10-N11-C14 | 120.8 | 119.1 | 118.1 |
| C13-O17 | 1.232 | 1.255 | 1.225 | C2-N12-C13 | 123.5 | 123.5 | 126.1 |
| C14-O15 | 1.399 | 1.422 | ----- | N12-C13-C14 | 116.7 | 116.9 | 115.7 |
| C23-C24 | 1.387 | 1.402 | 1.393 | N12-C13-O17 | 123.2 | 123.4 | 120.9 |
| C23-C28 | 1.394 | 1.41 | 1.393 | C14-C13-O17 | 119.9 | 119.5 | 123.4 |
| C24-C25 | 1.38 | 1.392 | 1.369 | N11-C14-C13 | 107.2 | 107.5 | 112.7 |
| C24-Cl33 | 1.818 | 1.837 | 1.742 | N11-C14-O15 | 110.6 | 110.7 | ----- |
| C25-C26 | 1.387 | 1.4 | 1.377 | C13-C14-O15 | 110.2 | 109 | ----- |
| C26-C27 | 1.386 | 1.399 | 1.373 | C10-C23-C24 | 123.8 | 124.4 | 124 |
| C27-O28 | 1.385 | 1.396 | 1.384 | C10-C23-C28 | 118.7 | 118.4 | 121.6 |
| CC | 0.994 | 0.995 | C24-C23-C28 | 117.4 | 117 | 118.1 | |
| C23-C24-C25 | 122.3 | 122.5 | 121 | ||||
| C23-C24-Cl33 | 120.4 | 120.5 | 120.8 | ||||
| C25-C24-Cl33 | 117.2 | 116.8 | 117 | ||||
| C24-C25-C26 | 119.1 | 119.1 | 120.6 | ||||
| C25-C26-C27 | 119.9 | 119.9 | 119.4 | ||||
| C26-C27-C28 | 119.9 | 119.9 | 120.6 | ||||
| C23-C28-C27 | 121.1 | 121.3 | 120.3 | ||||
| CC | 0.94 | 0.946 |
Note: CC-Correlation Coefficient.
Table 1: Selected bond length (Å) and bond angles (deg) values for Lormetazepam.
From Table 2, it is noticed that calculated atomic charges of Lormetazepam are not exactly the same and hence variations in the dipole moment values were observed. The dipole moment value obtained from RHF is higher (5.5099 Debye), whereas by B3LYP method gives small dipole moment values (3.3612 Debye). This dipole moment value discrepancy is mainly attributed to the variation of atomic charges.
| Atom numbering | Mulliken charge | |
|---|---|---|
| RHF/6-31G (d,p) | B3LYP/6-31G (d,p) | |
| C1 | -0.191213 | -0.124804 |
| C2 | 0.358349 | 0.265217 |
| C3 | -0.068398 | 0.099823 |
| C4 | -0.106262 | -0.117102 |
| C5 | -0.330458 | -0.235878 |
| C6 | -0.136663 | -0.101423 |
| C10 | 0.249031 | 0.059717 |
| N11 | -0.478789 | -0.327269 |
| N12 | -0.962897 | -0.638214 |
| C13 | 0.797769 | 0.515731 |
| C14 | 0.226436 | 0.094535 |
| O15 | -0.768291 | -0.620708 |
| O17 | -0.661035 | -0.499483 |
| C18 | -0.21588 | -0.251807 |
| Cl22 | 0.086948 | 0.059675 |
| C23 | -0.004872 | 0.077335 |
| C24 | -0.307079 | -0.248797 |
| C25 | -0.164659 | -0.116302 |
| C26 | -0.192571 | -0.116867 |
| C27 | -0.205387 | -0.134121 |
| C28 | -0.171971 | -0.122102 |
| Cl33 | 0.100009 | 0.067373 |
| Dipole moment (Debye) | 5.5099 | 3.3612 |
Table 2: Mulliken atomic charges.
Molecular orbital indices
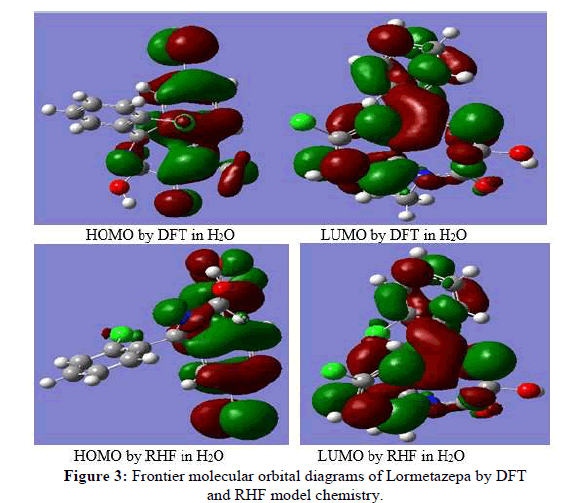
Nowadays, the Ab Initio and DFT based quantum chemical descriptors have provided the very useful information about the biochemical important molecules to explain their chemical activity behavior and to use them in the design of the new agent/drug used in cancer treatment. In this context the calculated quantum chemical indices EHOMO, ELUMO, EL-EH ionization potential, electron Affinity, electronegativity and hardness, are given at Table 3 for 6-31G (d,p) basis set in gas phase and in aqueous phase. The important point to be considered in the energy level terms is gap, between the HOMO and LUMO energies for the study molecule. The concept of the energy gap LUMO-HOMO to develop theoretical models have used by Cherry [20], which is capable of explaining the structure and conformation barriers in many molecular systems qualitatively. Low absolute values of the energy band gap (ΔE) gives more stability, because the energy to remove an electron from the last occupied orbital will below [21]. According to the data in Table 3 there is a good correlation in LUMO-HOMO energy gap by these methods in gas phase and in aqueous phase it can be seen that (ΔE) of the study molecule is low by B3LYP method, LUMO-HOMO gap is (0.1460 ev) whereas is (0.4122 ev), by RHF method in gas phase and (ΔE) in aqueous phase is low than in gas phase as data shown in Table 3. In many chemical reactions and physicochemical properties of compounds, it has been proven that the local electron densities or charges are important [22]. In simple molecular orbital theory approaches, the HOMO energy (EHOMO) is related to the IP by Koopmanns’ theorem and the LUMO energy (ELUMO) has been used to estimate the Electron Affinity (EA). The higher HOMO energy which corresponds to the more reactive molecule in the reaction with electrophile, while lower LUMO energy is essential for molecular reactions with nucleophile [23]. If ‐EHOMO ≈ IP and ELUMO ≈ EA, then the average value of the HOMO and LUMO energies is related to the electronegativity (φ) defined by Mulliken with φ=IP+EA/2. In addition, the HOMO‐LUMO gap is related to the hardness (η), η=ELUMO-EHUMO/2. According to the data in Table 3 the molecule has higher HOMO energy by DFT (-0.2486) than RHF(-0.3454) in the gas phase and in aqueous phase also HOMO energy greater than in gas phase. This results explain that the molecule is more reactive with electrophiles in aqueous phase. The molecular orbitals of study molecule in aqueous phase can be illustrated in the following Figure 3.
| Method | EHOMO ev | ELUMO ev | ΔE (L-H) ev | Ionization potential ev | Electron affinity ev | Electro negativity (φ) ev | Hardness ev |
|---|---|---|---|---|---|---|---|
| RHF/6-31G (d,p) in gas phase | -0.3454 | 0.0668 | 0.4122 | 0.3454 | 0.0668- | 0.1393 | 0.2061 |
| B3LYP/6-31G (d,p) in gas phase | -0.2486 | -0.0726 | 0.146 | 0.2486 | 0.0726 | 0.1606 | 0.073 |
| RHF/6-31G (d,p) in aqueous phase | -0.3445 | 0.0693 | 0.4138 | 0.3445 | 0.0693- | 0.1376 | 0.2069 |
| B3LYP/6-31G (d,p) in aqueous phase | -0.2475 | -0.072 | 0.1455 | 0.2475 | 0.072 | 0.1597 | 0.0727 |
Table 3: The calculated electronic properties of the study molecule using RHF/6-31G and B3LYP/6-31G methods.
Conclusion
The RHF and DFT calculations carried out using standard 6‐31G basis set gives a reasonable fit for molecular geometries assigned experimentally. A thorough analysis of the most important atomic charge, allowed us to explain electonegativity and electropositivity of the atoms of benzodiazepines RHF and DFT calculated reactivity descriptors: EHOMO, ELUMO, ΔE(L-H) electron affinity, ionization potential, electronegativity, dipole moment and hardness show very similar reactivity descriptor values and yield reasonable agreement with the relevant experiment reactivity results. In general, theoretical results are in complete agreement with observed experimental reactivity, confirming the reliability of the method employed here.
References
- Sternbach LH. J Med Chem. 1979; 22(1): p. 1-7.
[Crossref] [Google Scholar] [PubMed]
- Bell SC, Childress SJ. J Org Chem. 1962; 27(5): p. 1691-1695.
- Greenblatt DJ, Shader RI. Can J Neurol Sci. 1980; 7(3): p. 269-270.
[Crossref] [Google Scholar] [PubMed]
- D. Greenblatt, R Shader, M. Divoll, et al. Br J Clin Pharmacol. Wiley Interscience; 1981; 11(1): p. 11-16.
- Di Braccio, M Grossi, G Roma G, et al. Eur J Med Chem. 2001; 36(11-12): p. 935-949.
[Crossref] [Google Scholar] [PubMed]
- Kieć-Kononowicz, K Karolak-Wojciechowska, J Müller CE, et al. Eur J Med Chem. 2001; 36(5): p. 407-419.
[Crossref] [Google Scholar] [PubMed]
- Crupi V, Majolino D, Mondello MR, et al. J Pharm Biomed Anal. 2002; 29(6): p. 1149-1152.
[Crossref] [Google Scholar] [PubMed]
- Jadidi K, Aryan R, Mehrdad M, et al. J Mol Struct. 2004; 692(1-3): p. 37-42.
- Cascade E, Kalali AH. Psychiatry (Edgmont). 2008; 5(9): p. 21.
[Google Scholar] [PubMed]
- Cloos JM, Ferreira V. Curr Opin Psychiatry. 2009; 22(1): p. 90-95.
[Crossref] [Google Scholar] [PubMed]
- Marienfeld CB, Tek E, Diaz E, et al. Psychiatr Q. 2012; 83: p. 521-529.
- Paul Y, Tyagi S, Singh B. Int J Pharma and Bio Sci. 2011; 2: p. 20.
- Kaur NA. Int J Pharm Biol Sci. 2013; 4: p. 366-373.
- Gatzonis SD, Angelopoulos EK, Daskalopoulou EG, et al. Drug Alcohol Depend. 2000; 59(1): p. 95-97.
[Crossref] [Google Scholar] [PubMed]
- Nawrocka W, Sztuba B, Opolski A, et al. Arch Pharm (Weinheim). 2001; 334(1): p. 3-10.
[Crossref] [Google Scholar] [PubMed]
- Berezhnoy D, Baur R, Gonthier A, et al. J Neurochem. 2005; 92(4): p. 859-866.
[Crossref] [Google Scholar] [PubMed]
- Muthu S, Prasath M. Ann Fac Eng Hunedoara-Int J Eng. 2012; p. 10(3).
- Gilli G, Bertolasi V, Sacerdoti M, et al. Acta Crystallogr. B: Struct Crystal Crystal Chem. 1977; 33(8): p. 2664-7.
- Gece G. Corros Sci. 2008; 1;50(11): p. 2981-2992.[ Crossref]
- Karelson M, Lobanov VS, Katritzky AR. Chem Rev. 1996; 96(3): p. 1027-1044.
[Crossref] [Google Scholar] [PubMed]
- Rauk A. 2001. Orbital Interaction Theory of Organic Chemistry, 2nd Edn John Wiley and Sons: New York, Vol.34.
- Mulliken RS. J Chem Phys. 1934; 2(11): p. 782-93.
- Parr RG, Pearson RG. J Am Chem Soc. 1983; 105(26): p. 7512-7516.