Research Article - Der Pharma Chemica ( 2018) Volume 10, Issue 1
A Comprehensive DFT Study of Wurtzite ZnO
Benkrima Yamina1*, Achouri Abderrahim1, Bentouila Omar2 and Benmebrouk Lazhar3
1Department of Matter Sciences, Lenreza Laboratory, Faculty of Mathematics and Matter Sciences, Kasdi Merbah Ouargla University, Ouargla 30000, Algeria
2Department of Matter Sciences, Lenreza Laboratory, Optoelectronics Team, Faculty of Mathematics and Matter Sciences, Kasdi Merbah Ouargla University, Ouargla 30000, Algeria
3Laboratory of Radiation and Plasma and Surface Physics, Ouargla 30000, Algeria
- Corresponding Author:
- Benkrima Yamina
Department of Matter Sciences, Lenreza Laboratory
Faculty of Mathematics and Matter Sciences
Kasdi Merbah Ouargla University, Ouargla 30000, Algeria
Abstract
The polar ZnO surfaces have received wide interests due to their higher activity than the non-polar facets in catalysis, photo-catalysis and gas sensitivity. However, the theoretical study on the relative stability of the polar ZnO surfaces is still limited. In this work, Am calculate the surface energy of the polar ZnO(0001)-Zn and Zn( ̅)-O surfaces. The Density-Functional Theory (DFT) method shows that the ZnO( ̅)- O terminal is more stable than the ZnO(0001)-Zn terminal because the polarizability of surface O-2 is higher than that of surface Zn+2, which is in good agreement with the experimental results. The density of states shows the three surfaces of ZnO-O are better than that of the surface in bulk; this is what makes them qualified in the field of catalysis.
Keywords
ZnO(000͞1)-O surface, ZnO(0001)-Zn surface, DFT, Catalysis
Introduction
Zinc Oxide (ZnO) is an acidic compound naturally occurring as the rare mineral zincite, which crystallizes in the hexagonal wurtzite structure P63mc. The mineral zincite was discovered in 1810 by Bruce in Franklin (New Jersey, USA), ZnO is a group (IIVI) semiconductor material widely applied in optoelectronic because of its wide band gap (3.3 ev) [1], high chemical stability, high order transmittance and piezoelectric properties plane.
ZnO crystals exhibit several typical surface orientations. The most important surface are the (0001) basal plane and (000͞1), (101͞0) and (112͞0) (prism planes) and (112͞1) (pyramidal plane) crystal faces. In principle, the (0001) planes are terminated by Zn atoms only, and the (000͞1) planes are terminated by O. ZnO is also a bio safe and biocompatible material, with can be used for biomedical application [2]. The calculated surface energy is only an estimated value by the energy between the surface with and without hydrogen passivation. Therefore, a more direct calculation of the surface energy of ZnO polar surface is requested from a theoretical point of view. Theoretically, the surface energy is defined as the energy difference between the surface and bulk for one unit area. In the ab initio calculations, it is very convenient to calculate the surface energy of a surface with a symmetric opposite surfaces. An infinite slab with two symmetric surfaces can be built, and the surface energy is normally [3,4]:
S= (Eslab-n*Ebulk)/2A (1)
Where, S is the surface energy and Eslab is the energy of the slab, n is the atomic number of the slab and Ebulk is the energy per atom in the bulk, A is the area of the slab. In this work, the separated surface energies of the ZnO (0001)-Zn terminal and the ZnO (000͞1)-O terminal we adopt the Density Functional Theory (DFT) calculation by using the program SIESTA, within the Generalized Gradient Approximation (GGA) [5].
Theoretical approaches
The present calculations are based on DFT within the Generalized Gradient Approximation (GGA) [5], which is parameterized by Perdew, Burke and Ernzerhof (PBE) [6]. The calculate basis with a cutoff energy of 200 eV. We first optimize the bulk wurtzite ZnO structure, yielding the following lattice parameters: a=b=3.284 Å, c=5.33 Å. These lattice parameters are in very good agreement with the experiment results [7], a=3.2496 Å and c=5.2042 Å. To prevent unphysical charge transfer between the top and bottom slab surfaces, pseudohydrogens with fractional charges are used. A 6 × 6 × 1 Monk horst–Pack mesh is used for the Brillouin zone integration.
Result and Discussion
Unit cell structure
Unit cell structure ZnO stable (B4) structure having hexagonal primitive unit cell with space group C4 6v P63mc. Each primitive unit cell of ZnO consists of four atoms where two Zn atoms are at the positions (1/3, 2/3, 0), (1/3, 2/3, 1/2) and O atoms at positions (1/3, 2/3, μ), (1/3, 2/3, μ+1/2). μ is the internal parameter of the B4 phase that determines the bond-length (AnionCation bond length) parallel to c-axis divided by the c-lattice parameter.
The bulk parameters of ZnO are calculated to be a=3.284 Å, c=5.333 Å and Eg=0.65 ev which is in reasonable agreement with the previous DFT calculation with a=3.283 Å, c=5.289 Å [8].
Our results with GGA are in good agreement to another theory results [9-11], which is lower than the experimental value in band gap. This is regarded as a spread problem of DFT calculations. Table 1 shows the results of a, b, c/a and band gap (Eg).
| Method | Code | a (Å) | c (Å) | c/a | Eg (ev) |
|---|---|---|---|---|---|
| This work | Siesta: GGA | 3.284 | 5.33 | 1.623 | 0.65 |
| Reference [9] | Transiesta: GGA | 3.288 | 5.27 | 1.603 | 1.02 |
| Reference [10] | Wien2k: GGA | 3.3 | 5.346 | 1.62 | 0.69 |
| Reference [11] | Wien2k: GGA | 3.24 | 5.2 | 1.602 | 1.2 |
Table 1: The calculated lattice parameters of ZnO in phase (wurtzite) in comparison with theoretical values available
Surface energy
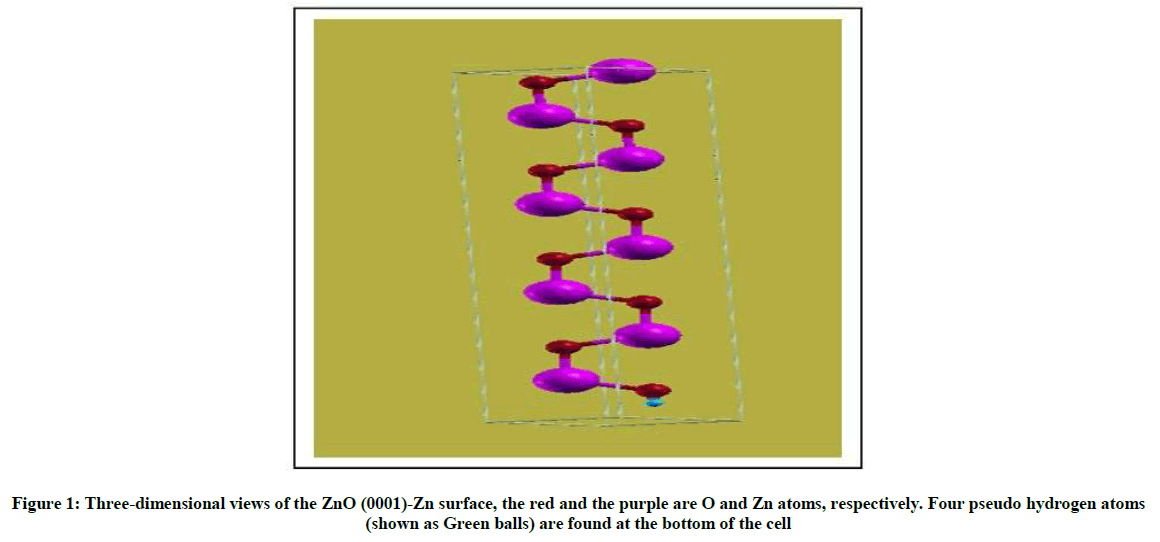
For material slab models, the smaller the surface energy is, the more stable the surface is our calculated surface energies are shown in Table 2, the surface energies of the 8-layer By comparison, we found that the surface energy of the Zn-polar (0001) surface is bigger than that of the Opolar (000͞1) surface, which shows that the ZnO-Zn surface is more active than the ZnO-O surface (Figure 1). This is in good agreement with Similar to the result of the theory [12].
| Method | Surface slab | Surface energy (J/m2) | |
|---|---|---|---|
| ZnO: Zn-polar (0001) | ZnO: O-polar | ||
| This work | 8 | 3.76 | 3.1 |
| Reference [11] | 8 | 2.283 | 2.273 |
Table 2: Surface energies of 8 layer- ZnO (000͞1) and ZnO (0001) surfaces
Band structure and density of states
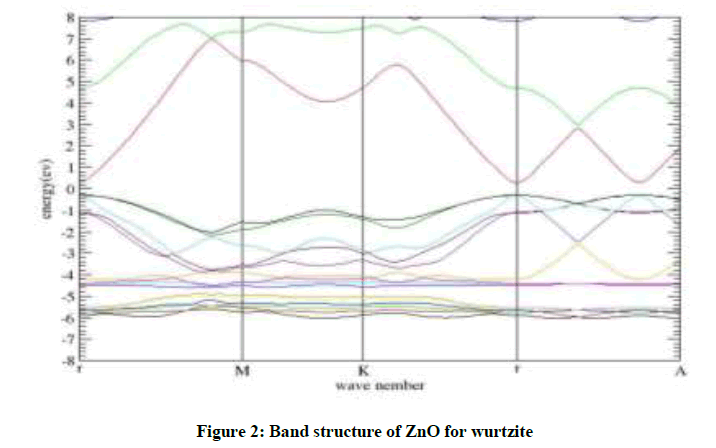
The band structure of ZnO in wurtzite is evaluated using calculated lattice parameters (a=3.284 Å, c=5.33 Å). It can be seen that the valence band maxima and conduction band minima lie on the same 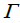 point, indicating direct band.
point, indicating direct band.
Calculated band gap values with GGA are smaller than experimental results indicating that this form of GGA is not sufficiently flexible to give consistent results for band gap energy similar to other forms of GGAs and LDA. Our calculated band gap value for wurtzite is about 60.00% less than that of experimentally [13], reported band gap values. This is in good agreement with similar to the result of the theory [11]. The band structure show in Figure 2.
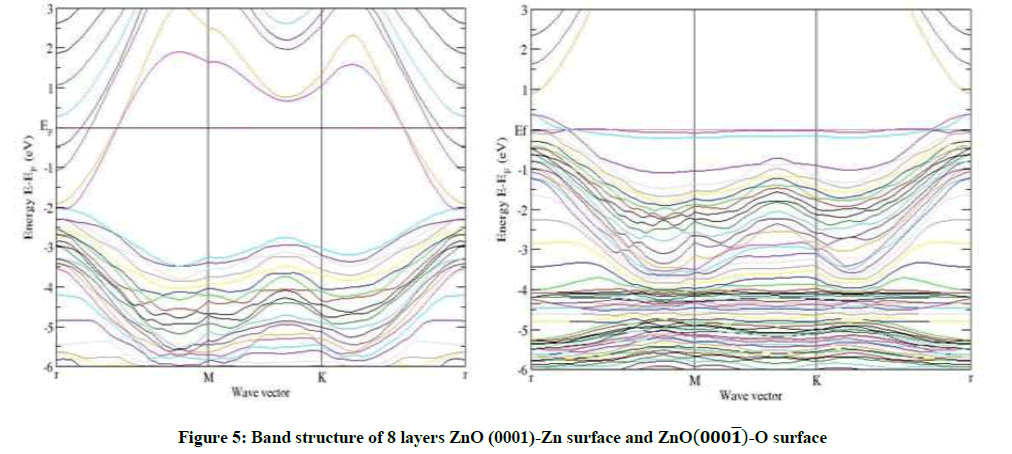
The electronic structures of the ZnO-Zn and ZnO-O surfaces are affected by surface termination. These polar surfaces have the same bulk structure, but they have different atomic compositions and different surface morphologies. Surface states are electronic states of the surfaces of materials. They are formed due to the sharp transition from solid material.
That ends with a surface and is found only at the atom layers closest to the surface. The termination of a material with a surface leads to a change of the electronic band structure from the bulk material to the vacuum. In this article, the nature of surface states has been investigated by comparing the surface band structures with pseudo hydrogen saturation. To study the surface states of the polar surface films, we have passivated only one surface at a time, that is, either the ZnO-Zn surface or ZnO-O surface is passivated.
Thus, we can make sure of the positions of the ZnO-Zn and ZnO-O surface states and then study them. Here, the ZnO-Zn and ZnO-O surface states are situated at the bottom of the conduction band and the top of the valence band, respectively. The ZnO-Zn surface declines a lot as a whole relative to the Fermi level and the ZnO-Zn surface states become steeper, while on the other hand the band structure of the ZnO-O surface rises a little as a whole relative to Fermi level and the ZnO-O surface states become flatter, but the valence bands dramatically change.
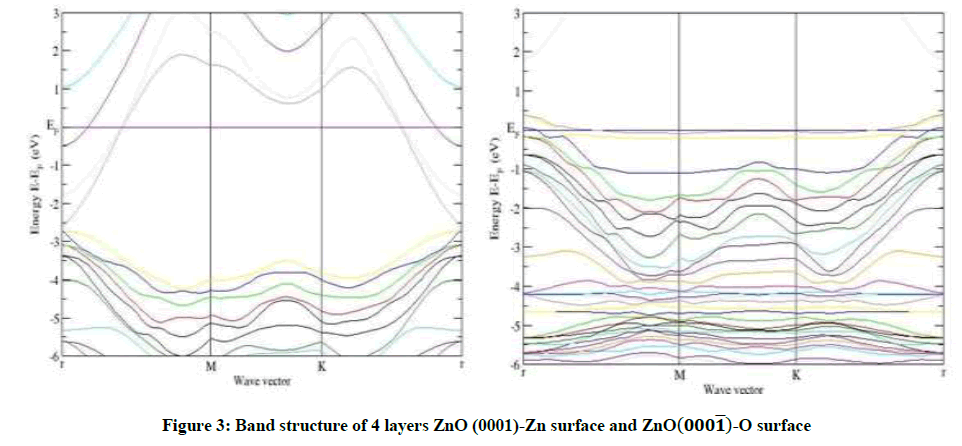
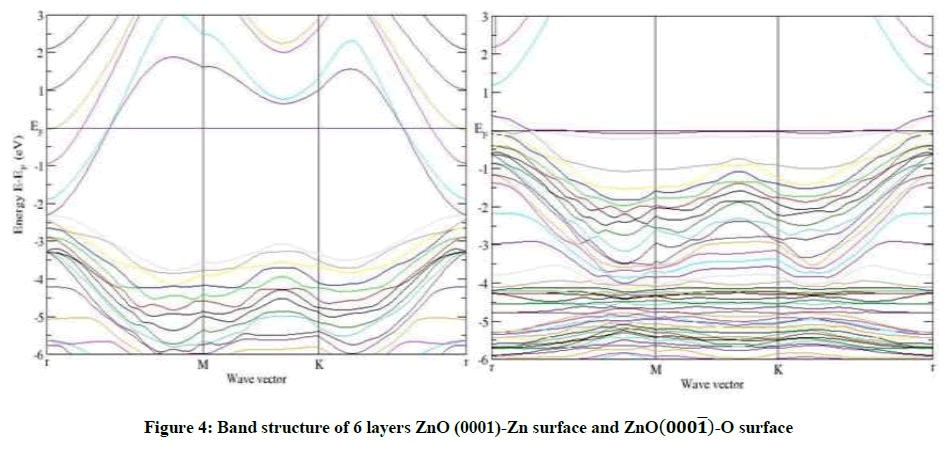
As an example, for 8 layers of ZnO-Zn surface in Figures 3-6, a narrow surface band gap about 3.32 eV exists above the top of the valence band. In addition, the Fermi level enters into the conduction band deeply, and partial surface states appear below the Fermi level. Therefore, the ZnOZn surface is of n-type conduction.
Characteristic completely different from the ZnO-Zn surface, the ZnO-O surface has a surface band gap about 0.6 eV, and the Fermi level shifts into the valence band, which predicts that the ZnO-O surface has p-type conduction behavior, this observation also applies to 4 layers and 6 layers of ZnO-O and ZnO-Zn in Figures 3-5. The calculated results are in good agreement with the theory and the experiment [14,15].
Density of states
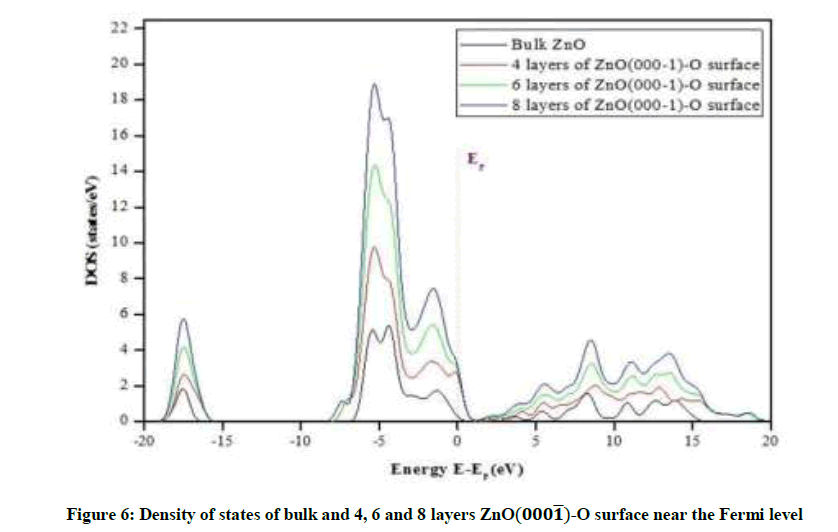
The Figure 6 At the bottom shows that the highest case density peak at Fermi level is close to the value: 3 states/eV for eight layers of ZnO-O, Followed by less summit is estimated at 2.8 states/eV for six layers and less than the previous peaks recorded in the case of the four layers are estimated at: 2.5 states/eV and case density values for the previous layers were also recorded in the conduction ring area near the Fermi level which seems to us to have roughly the same value, which is characterized by the presence of densities of cases in this region compared to the state of the surface in its solid state, the latter shows no value in this area, it was also noted the presence of small peaks of case densities in the transport ring area of the studied surfaces.
High peaks of case density were also recorded in the field from [4.4- to eV5-6] in each of the three surfaces of the surface ZnO-O and this is of course the ring of equivalence rich in the presence of electrons. In general, the case density of the three surfaces is more chemically active than the surface state in its solid state, in both the valence ring and the conduction ring, and that the increase in the value of the density relates to the number of layers formed for the surface, in other words, there is a positive relationship to the density of cases with the number of layers formed for the latter. The densest surfaces are the most stimulating surfaces.
Conclusion
We have performed density functional theory calculations to determine the structure properties of wurtzite ZnO (0001) and (000͞1) surfaces. The surface energy of Zn-polar (0001) is bigger than that of O-polar (000͞1). Say the ZnO-O surface is more stable than the ZnO-Zn surface. ZnO in wurtzite phases is a direct band gap semiconductor. The three surfaces of ZnO-O are better than that of the surface in bulk; this is what makes them qualified in the field of catalysis.
References
- C. Jagadish, S. Pearton, Zinc Oxide Bulk, Thin Films and Nanostructures, Processing, Properties and Application, 1st Edi, Elsevier Science, 2006.
- C. An-Jen, One dimensional Zinc Oxide Nanostructures for Optoelectric Applications: Solar Cells and Photodiodes, PhD of Philosophy, Auburn, Alabama, 2008.
- M. Ramamoorthy, D. Vanderbilt, R.D. King-Smith, Phys. Rev. B., 1994, 49, 16721.
- V. Fiorentini, M. Methfessel, J. Phys. Condens Matter., 1996, 8, 6525.
- M.C. Payne, M.P. Teter, D.C. Allan, T.A. Arias, J.D. Joannopoulos, Rev. Mod. Phys., 1992, 64, 1045.
- J.P. Perdew, K. Burke, M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
- A. Cimino, G. Mazzone, P. Ports, Z. Physik. Chem., 1964, 41, 154.
- A. Schleife, F. Fuchs, J. Furthmuller, F. Bechstedt, Phys. Rev. B., 2006, 73, 245212.
- A. Srivastava, N. Tyagi, Int. J. Mod. Phys. B., 2012, 11, 1250035.
- A. Mokadem, M. Bouslama, O. Benhelal, A. Assali, M. Ghaffour, Z. Chelahi Chikr, K. Boulenouar, A. Boubaia, Int. J. Mod. Phys. B., 2014, 28, 1250035.
- B. Ul-haq, A. Afaq, R. Ahmed, S. Naseem, Int. J. Mod. Phys. C., 2012, 23, 1250043.
- Z. Yufei, G. Zhiyou, G. Xiaoqiother, C. Dongxing, D. Yunxiao, Z. Hongtao, J. Semiconductors., 2010, 31, 082001.
- J.A. Camargo-Mart Inez, R. Baquero, Revista Mexicana de., 2013, 59, 453.
- C.J. Zhou, J.Y. Kang, J. Mater. Sci. Mater. Electron., 2008, 19, S229.
- A. Urbieta, P. Fernandez, C. Hardalov, Mater. Sci. Eng. B., 2002, 91/92, 345.